Når vi skal illustrere kurver (eller kurvede flater) har vi behov for noen smidige verktøy for å framstille justerbare buede linjer uten å måtte angi hvert enkelt punkt. Du finner slike tegneverktøy i de fleste ikke-trivielle tegneprogrammer. Her skal vi se på to elegante, beslektede, innfallsvinkler lansert av to franskmenn som var ansatt i bilindustrien: Paul de Casteljau (Citroën) og Pierre Bezier (Renault). de Casteljau hadde sin løsning klar på slutten av 1950-tallet. Det er Beziers løsning som ble publisert noen år senere som har gitt navn til kurven. Trolig fordi han var flinkere til å publisere.

Jeg har tatt med dette eksempelet av to grunner: For det første har de Casteljaus løsning en elegant algoritmisk begrunnelse. For det andre fordi Bezier koplet denne til en etablert matematisk verktøykasse.

de Casteljau

Vi starter med de Casteljau siden det er her vi finne de grunnleggende algoritmiske resonnementene. Det første vi gjør er å introdusere en enkel og, viser det seg, fruktbar måte å beskrive linjestykker på. Vanligvis angir vi endepunktene og sier at en linje i planet går mellom to punkter, P0 og P1, og vi kan gjøre nødvendige beregninger og uttegninger ved hjelp av de respektive x- og y-verdiene.(x0, y0) og (x1,y1).

I sine resonnementer bruker de Casteljau en parametrisk framstilling av en linje:

P(t)=(1-t)P0+tP1

Vi ser at når t=0 så blir P=P0, og når t=1 så blir P=P1. Ved å øke t suksessivt fra 0 til 1 så vandrer vi (P) langs linjestykket.

Det finurlige i de Casteljaus algoritmiske resonnement er illustrert i tabellen nedenfor. Punktene P0, P1, P2, P3 ligger i ro, men de andre punktene er avhenig av t. Punktet P(t) vil beskrive en kurve.

	P(t)=(1-t)P0+tP1
	P(t)=(1-t)A(t)+tB(t) og: A(t)=(1-t)P0+tP1 B(t)=(1-t)P1+tP2 Vi setter inn og får: P(t)=(1-t)2P0+2t(1-t)P1+t2P2
	P(t)=(1-t)D(t)+tE(t) og: D(t)=(1-t)A(t)+tB(t) E(t)=(1-t)B(t)+tC(t) og: A(t)=(1-t)P0+tP1 B(t)=(1-t)P1+tP2 C(t)=(1-t)P2+tP3 Vi setter inn og får: P(t)=P0(1-t)3+3P1t(1-t)2+3P2t2(1-t)+P3t3

Du kan flytte de blå punktene (P₀,P₁,P₂,P₃) med musa. Det røde punktet, P(t), flytter seg fam og tilbake langs kurven. De små svarte prikkene markerer A,B,C,D,E.

Det er et par ting som er nyttige å merke seg:

• Kurven starter (t=0) i P0 og den slutter (t=1) i P3.
• Kurven kommer aldri innom P₁ og P₂.
• Kurven kommer aldri utenfor det konvekse polygonet som er definert av P0,P1,P2,P3.
• Vektoren P0->P1 er den deriverte i P0, og vektoren P2->P3 er den deriverte i P3.

Hvis vi deriverer uttrykket:

P(t)=P0(1-t)3 + 3P1t(1-t)2 + 3P2t2(1-t) + P3t3

får vi:

P'(t)=3P0(-t2+2t-1) + 3P1(3t2-4t+1) + 3P2(-3t2-6) + 3P3(t2)

Det vil si at:

P'(0)=3(P1-P0)
P'(1)=3(P3-P3)

Og vi har altså kontroll over retningen i endepunktene hvis vi vil skjøte kurver, se nederst på siden.

Bezier

Bezier angriper problemet på en litt annen måte. Han ønsker å finne et tredjegrads polynom:

B(t)=at3 + bt2 +ct +d

der den deriverte blir:

B'(t)=3at2+2bt+c

Han bestemmer seg (?) videre for at

B'(0)=3(P1-P0)
B'(1)=3(P3-P2)

(Hvilket var det vi kunne utlede fra de Casteljaus algoritme ovenfor !)

For å finne a,b,c,d må vi løse dette ligningssystemet med hensyn på a,b,c,d:

d=P0
a+b+c+d=P3
c=3(P1-P0)
3a+2b+c=3(P3-P2)

Vi løser og får:

a=-P0+3P1-3P2+P3
b=3P0-6P1+3P2
c=3P1-3P0
d=P0

Vi setter opp og ordner polygonet:

B(t)=P0(-t3+3t2-3t+1) + P1(3t3-6t2+3t) + P2(-3t3+3t2) + P3(t3)

eller:

B(t)=P0(1-t)3 + 3P1t(1-t)2 + 3P2t2(1-t) +P3t3

som jo er det samme som de Casteljau kom fram til!.

Vanligvis skrives Bezier-formelen for 4 styrepunkter slik:

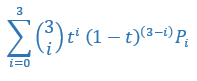
Vi kan generalisere denne med hvor mange styrepunkter vi vil:

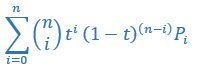
Binomialkoeffisienten er definert slik

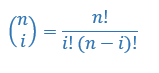
Vi finner dem igjen i Pascals trekant:

         1
      1     1
    1    2    1
  1    3   3    1
1   4    6    4   1

En av fordelene med denne kurven, enten vi kaller den Bezier eller de Casteljau, er at vi har kontroll over hvordan vi skal kunne glatte skjøtede kurver:

Vi framstiller eksemplene nedenfor slik du ofte finner dem i tegneprogrammer med "handtak" som vi kan ta tak i for å endre kurveformen. Enden på disse handtakene er i prinsipp punktene P₁ og P₂.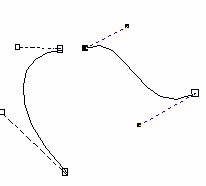

	Ingen kontinuitet. De to kurvesegmentene har ikke noe felles punkt.
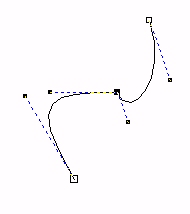	De to kurvesegmentene har et felles punkt. Kurvene henger sammen men har en tydelig knekk. De deriverte (for høyre segment og venstre segment) i dette punktet er forskjellige både i retning og størrelse.
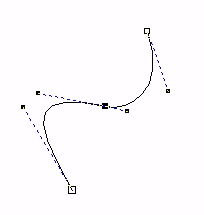	De to kurvesegmentene har et felles punkt, og skjøten er ganske glatt. De deriverte i dette punktet har samme retning.
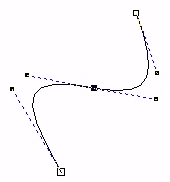	De to kurvesegmentene har et felles punkt, og skjøten er glatt. De deriverte i dette punktet har samme retning og samme størrelse