Dart er et engelsk spill som går ut på å kaste piler på en blink. Vi skal bruke dette spillet som et eksempel på organisering av data og en enkel rekusjonsalgoritme.

De enkelte feltene på blinken gir ulike antall poeng:

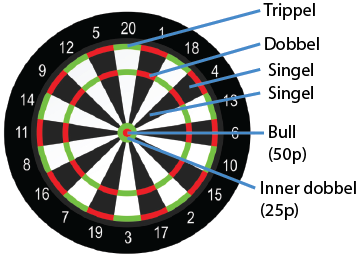
Dart spilles av to spillere som kaster runder med 3 piler annenhver gang. Når spillet starter har begge spillerne 501 poeng. Poengene de skårer på hver pil trekkes fra denne summen og det er den som kommer først til 0 som vinner.

Det er en komplikasjon med dette: De siste poengene må oppnås med en "dobbelt"-verdi eller en sentrumstreff(Bulls eye). En avslutning kan oppnås med med 1,2 eller 3 piler i det som i så fall blir siste runde. Vi kommer tilbake til dette.

Mulige poeng

Det første vi gjør er å finne alle mulige poeng som kan oppnås med en pil. Hvis du ser på tavla ovenfor ser du at det er markert 20+20+20+20+2= 82 felt. Flere av disse gir samme resultat. De to singel-feltene for hvert talltriangel gir det samme, og vi kan oppnå det samme f.eks. med en singel 6, en dobbel 3 eller en trippel 2. Vi forsøker å sette opp en algoritme som gir oss en lista av mulige utfall av et pilkast slik at vi har materiale for å finne kastsekvenser. Vi dropper helbom (0 poeng).

// mulige pilpoeng
var PP

function finnPilpoeng(){
  PP=[];// alle
  for (var ix=1; ix <=20; ix++){
    PP.push(2*ix);
  }
  for(var ix=1; ix <=20; ix++){
    if(PP.indexOf(3*ix)==-1)
      PP.push(3*ix);
  }
  for(var ix=1; ix <=20; ix++){
    if(PP.indexOf(ix)==-1)
      PP.push(ix);
  }
  // senter
  PP.push(25);
  PP.push(50);

  PP.sort(function(a,b){return a-b});
  visPilpoeng();
}

Hvis vi går gjennom PP og finner (i proritert rekkefølge uten gjentagelse): singelverdier, dobbeltverdier og trippelverdier:

Hvis vi ser bort fra helbom har vi altså 43 mulige utfall av et pilkast.

Avslutning

Gode dartspillere er ikke bare støe på hånden, de er også gode til å regne i hodet og til å finne gode algoritmer for å avslutte et spill. Strategien deres er selvsagt påvirket av motstanderens poengsum og av hva de vet at de selv er gode eller mindre gode på. Denne delen av strategien får vi overlate til dem. Vi skal se litt på det tallmaterialet de har som rammer for sin planlegging, og se om vi kan lage en algoritme som viser hva som egentlig foregår i hodet på en dartspiller. Hvis du ser trente dartspillere i aksjon vil du se at de av og til nøler et sekund, eller kanskje to, før de starter den potensielle sluttrunden, og spesielt dersom den første pila i avslutningsrunden ikke går som planlagt.

Anta at en spiller må skåre N poeng: Er det mulig å avslutte med 1, 2 eller 3 piler?, og vilke alternativer finnes ? Vi må huske på at det siste kastet må være en dobbel eller en bulls-eye (som jo også er en dobbel rent numerisk sett).

Vi vil finne kombinasjoner av kast som er nødvendig for å få tallet ned til 0. Vi går ut fra at vi har følgende globale variable:

// poengmuligheter for et kast som vi lagde ovenfor
var PP;
// mulige resultat, en array av arrays med 1,2 eller tre pilpoenger
var resListe;
// f.eks: 3 (av flere mulige) kastsekvenser for å oppnå summen 6:
// [[2,2,2],[4,2],[6]]

Vi forsøker oss med en rekursiv algoritme:

function finnKastSekvenser(totalsum,piler){
  // piler =3,2 eller 1
  // ingen funnet
  resListe=[];
  var res=[];
  // sett opp tomt resultat
  for(var ix=0; ix < piler; ix++)
    res.push(0);
  finnKast(totalsum,piler-1,res,totalsum);
  visResultatListe();
}
function finnKast(restSum,kastnr,result,totalsum){
  for (var ix=0; ix < PP.length; ix++){
    if(PP[ix] <= restSum){
      result[kastnr]=PP[ix];  
      var s=sum(result);
      if(s==totalsum){
        // sjekk om resultatet er ok: 
        //  minst en dobbel 
        //  finnes ikke fra før
        //  fjern 0er
        if(resultIsOk(result))
          resListe.push(result);
      }
      else if(kastnr >= 0){
        //Merk at vi bruker slice() for sende en kopi
        //av resultatet så langt
        finnKast(totalsum-s,kastnr-1,result.slice(),totalsum);
      }
    }
  }
}

Resultatet for f.eks. finnKastSekvenser(12,2) blir:

resListe=[[12],[2,10],[8,4],[6,6]]

Vi bryr oss ikke om detaljer i formatering av utskriften her. Det er litt fingetrøbbel med sekvens innen en løsning og identifisering av doble, triple, single og BULL, men vi har alle dataene tilgjengelig for dette arbeidet klart i form av pilpoeng. Du kan teste løsningen nedenfor.

Anta at vi tester med maks 3 piler: Da får vi opp en liste med muligheter og kan legge en plan. Hvis vi bommer med den første pila, vil vi i noen tilfeller kunne bruke den samme tabellen til å planlegge en avslutning. Ofte vil imidlertid missen føre til at vi må skrive inn et nytt tall, det vi hadde minus det vi fikk, og lete etter en ny plan med 2 kast for det nye tallet.

Når det gjelder rekkefølgen og formen (D,T,singel) på de 2 første kastene når vi har 3 kast tilgjengelig kan formuleres på mange måter. Jeg har valgt å bruke singel-kast hvis mulig siden dette er det enkleste målet. En erfaren dartspiller ville sikkert ha forslag til forbedringer, på både rekkefølgen av rader og kolonner. Men husk at det må alltid ligge en dobbel eller Bull i den høyre kolonnen.

Vi har i og for seg laget en algoritme som finner fram til gode planer, men vi har neppe laget et operativt verktøy for en dartspiller. Kanskje det med litt endring kunne brukes som verktøy for en TV-kommentator?.