Fibonacci-tallene har fått sitt navn etter en italiensk matematiker som kalte seg Leonardo Fibonacci. I følge historien, slik den er beskrevet på Wikipedia, het han vistnok egentlig Leonardo Pisano Bigollo. Tallrekken har i all sin enkelthet opp gjennom årene fått mye oppmerksomhet av forskjellige grunner. Du finner litt om dette nederst på siden. Her skal vi primært bruke Fibonacci-tallene som eksempel på å illustrere to algoritmiske innfallsvinkler.
Tallrekken er veldig enkel: det neste tallet i rekka er summen av de to foregående. Vi kan begynne med tallene 0 og 1 og hvis vi fortsetter får vi: 0 1 1 2 3 5 8 13 osv.
Altså:
F0=0 F1=1 F2=1 F3=2 ... Fn=Fn-2 + Fn-1for n > 1
De 10 første tallene er: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34
Beregning
Vi vil lage og implementere en algoritme som skal regne ut det n'te fibonaccitallet. Vi ser av definisjonen at vi må holde styr på to tall, det siste tallet (t2) og det nest siste tallet(t1), og vi må ta vare på de to første tallene spesielt siden de ikke er laget etter "summen av de to foregående"-regelen men er definerte som 0 og 1.
// versjon 1
function fib(n){
if(n < 2)
return n;
var t1=0;
var t2=1;
var sum=0;
for(var i=1; i < n; i++){
sum=t1+t2;
t1=t2;
t2=sum;
}
return sum;
}
Løsningen over er gei nok, og er vel så effektiv som vi kan få det til. Det er imidlertid besnærende å se på en løsning som er svært kompakt og enkel:
// versjon 2
function fibR(n){
if(n < 2)
return n;
return fibR(n-1)+fibR(n-2);
}
Det vi har laget her er en rekursiv løsning, altså en funksjon som kaller seg selv. Formuleringen er så nærme vi kan komme selve definisjonen av fibonacci-tallene. Det er imidlertid åpenbart at versjon2, den rekursive, er langt mindre effektiv enn versjon1. Versjon2 krever ar vi beregner alle tall fra bunnen av, altså fra n=0, hver gang vi kaller funksjonen. Tallene blir slik for fibonaccitallene 0:9:
| Fibonacci tall nr | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Løkkerunder i funksjonen fib | 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Antall kall på fibR i den rekursive løsningen | 1 | 1 | 3 | 5 | 9 | 15 | 25 | 41 | 67 | 109 |
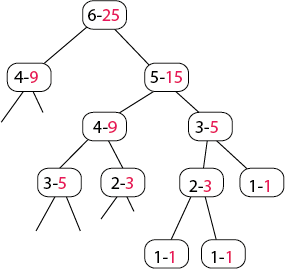
Antall ganger vi går i løkka i den første løsningen er lineært økende med fibonaccitall nummeret, men antall funksjonskall i den iterative løsningen er F(n)=F(n-1)+F(n-2)+1. Trestrukturen nedenfor illustrerer (deler av) hvordan den rekursive løsningen genererer fibonaccitall nummer 6. De svarte tallene er nummeret vi er ute etter og de røde er antall funksjonskall som skal til for å lage det.
Visualisering
Du vil finne mange eksempler av det som ofte kalles fibonaccis spiral. Her tegner vi kvadrater som har sidekanter lik tall i rekka (1,1,2,3,5,8,13,21,34,55), og vi ordner dem slik at vi visualiserer at kanten er summen av kantene i de to foregående. Til slutt lager vi en bue inne i hvert kvadrat.
Det gylne snitt
Vi kan ikke forlate fibonacci-tallene uten å kikke litt på det som omtales som "det gylne snitt". Et areal som er utformet med denne egenskapen blir oppfattet som den peneste og mest avbalanserte formen på et rektangel. Dette er et fenomen som er kjent, beskrevet og brukt av matematikere, designere og kunstnere langt tilbake i tid. I den greske antikken ble det beskrevet og noen mener det var et kjent fenomen i det gamle Egypt.

Høyden, b, og bredden, a, er satt opp etter følgende resonnement:

(a+b)/a = a/b
Vi vil kalle forholdet φ (phi)
φ=a/b
Vi setter inn i dette i (a+b)/a = a/b, og får en 2.gradsligning
φ2- φ -1 = 0Vi løser denne og får (avrundet til 6 desimaler):
φ ≈ 1.618033989
Og hva har så dette med Fibonacci-tallene å gjøre ?
Det viser seg at hvis vi betrakter Fn/Fn-1 så får vi følgende verdier for de første fibonacci-tallene:
Forholdet mellom to naboer i fibonacci-rekka konvergerer mot φ. Det er nok denne sammenhengen som gjør at Fibonacci-tallene, som jo i seg selv er en ganske enkel øvelse, her fått såpass mye fokus. Det er ett av mange eksempler på at temaer matematikken henger samme på en måte som ikke er åpenbar.
Men dette er jo pussig, eller ?: Du kan jo sjekke hva tallet(φ) blir hvis Fibbonacci hadde bestemt seg for at det første tall i rekka er 19 og andre tall er 36, i stedet for 0 og 1.
Foruten at det gyldne snitt som sagt har fått mye oppmerksomhet i forbindelse med design så viser det seg også at φ er et tall som dukker opp i forbindelse med fenomener og former i naturen. Du finner mange referanser til dette på nettet.
Det er matematikere som trekker fram det gyldne snitt som et tema i en faglig debatt om matematikken er noe vi har funnet på fordi det er nyttig, eller om den faktisk finnes i naturen. Jeg har ingen forutsetninger for å gå inne i denne debatten, men det er en interessant problemstilling.
