Dette er en klassiker som ble introdusert av en fransk matematiker, Édouard Lucas, på 1800 tallet. Øvelsen assosieres med en form for mental trening innen hindusimen. Så vidt jeg har greid å finne ut er dette ikke dokumentert(?).

Det er et godt eksempel på en effektiv rekursiv algoritme. Du må eksperimentere litt for å følge resonnementet nedenfor. Problemet er som følger:

Vi har tre pinner, A B C, og tre skiver som er satt opp slik: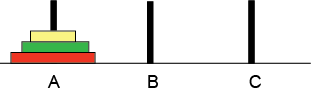
Vi skal flytte skivene slik at vi får denne situasjonen: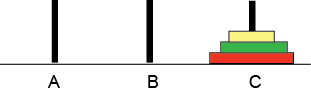

Det er tre regler for hvordan vi kan flytte:

1. Vi kan flytte bare en skive om gangen
2. Vi må ta den øverste skiva på en pinne og plassere den på toppen på en annen pinne
3. Ingen skive kan plasseres over en mindre skive

Gitt disse reglene kan du forsøke og flytte alle pinnne fra A til C for å få en ide om strategien. Du vil trenge 7 flytt.

Du vil se at, hvis vi ser bort fra å flytte en pinne direkte tilbake, vil vi hele tiden ha to lovlige flytt. Hvis vi skal lage og programmere en algoritme som løser problemet kunne vi velge en primitiv løsning der tester begge de lovlige flyttene i hver situasjon. Med et behov for 7 flytt vil vi tilsammen ha 2⁷ situasjoner. Vi må hele tiden sjekk hva som er mulig og det vanskelig å peke ut noen klar strategi. Det vil fort eskalere hvis vi begynner med flere ringer. Vi prøver å finne på noe lurere.

Rent metodisk er det slik at for å flytte 3 ringer fra A til C må vi flytte de to øverste ringene fra A til B og C må være tom. Det siste er vødvendig for at vi skal kunne ta den siste (største) ringen fra A til C. Når dette er gjort flytter vi de to gjenstående ringene fra B til C, med hjelp av den nå tomme A-pinnen.

Vi begynner med å betrakte flyttingene med 3 ringer:
AC,AB,CB,AC,BA,BC,AC

Utgangspunktet
Mellomlagrer på "ventepinnen B": AC, AB, CB
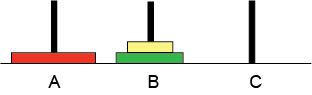AC
Henter fra "ventepinnen": BA, BC, AC

Vi får et helt tilsvarende resonnement (mellomlagring - flytt den store pinnen - hent på lageret)

for 2 pinner: AB - AC - BC

for 3 pinner: AC,AB,CB - AC - BA,BC,AC

for 4 pinner: AB,AC,BC,AB,CA,CB,AB, - AC - ,BC,BA,CA,BC,AB,AC,BC

Merk at "flyttingen til lager" begynner med AB for 2 pinner og 4 pinner, mens den begynner med AC for 3 pinner. Den rekursive funksjonen som fanger opp dette og gjør jobben er forbløffende enkel:

Anta at antall ringer 3, og pinnene ser slik ut:

var AntallRinger=3
var A = [3,2,1];
var B = [];
var C = [];

Funksjonen er slik, kalles med flytt(3,A,C,B)

function flytt(n, fraP, tilP, venteP){
  if (n <=0 )
    return;
  // sett n - 1 ringer på venteP
  flytt(n - 1, fraP, venteP, tilP);
  // foreta flyttingen
  tilP.push(fraP.pop());  
  // hent n-1 ringer fra venteP til tilP
  flytt(n - 1, venteP, tilP, fraP);
}

Test den i aksjon nedenfor.(Merk at animasjonene utføres etter at jobben er gjort og sekvensene er logget )

Som du vil se er antall flytt lik 2ⁿ-1, der n er antall pinner.

Hvis vi vender tilbake til de mulige røttene i hindusimen, er det vel forståelig at det skal ikke så mange ringer til før øvelsen er ganske krevende med tanke på konsentrasjon og utholdenhet. Og det var kanskje det prestene skulle trenes i, ikke vet jeg.