Nedenfor finner du en utfordring. Det du skal gjøre er å klikke på de fargede knappene under tegneflaten og ordne de fargede strekene slik at de danner et kvadrat. Prøv deg litt fram og se om du kommer i nærheten av det som er beregnet som minimum antall klikk. Det vi skal se nærmere på under spillet er hvordan vi kan regne ut nettopp dette tallet.

Rent algoritmisk kan du betrakte dette som en øvelse i å holde styr på vinkler.

Når vi skal gå løs på å analysere en oppgave baserer vi oss på følgende data:

// de 4 vinklene i figuren legges inn i en array
var vinkel=[0,0,0,0];
// vinkelendring (grader) ved et klikk
var dv=10;

Minimum klikk

Så fort en ny oppgave lages med tilfeldige vinkler regner programmet ut hva som er minimum antall klikk for at figuren skal bli et kvadrat.

Det er et par grunnleggende observasjoner ligger til grunn for analysen:

• Det er ingen grunn til å endre den første vinkelen. Endringer her vil bare rotere kvadratet
• De 3 andre vinklene må være like, og rette

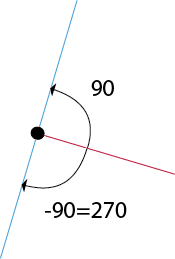
Vi antar at vi har tegnet den røde linja. Vi plasserer origo i enden av linja og betrakter forlengelse av den røde linja som x-aksen. Vi må snu oss 90 eller 270 grader for å tegne den blå. Hvis vi skal kunne forme et kvadrat må vi være konsekvente og velge samme vinkel for hver av tre siste hjørnene.

Den første linja kan ha vilken retning den vil. Hvis den ikke er vannrett eller lodrett vil det bare bidra til at kvadratet i sin helhet er rotert, men det er likevel et kvadrat.

Koden nedenfor implementerer den vurderingen vi må gjøre når vi planlegger korteste (færrest mulig klikk) vei til målet. Nå vi betrakter figuren er det ikke altid like enkelt å se den korteste veien. Dessuten er det her som alltid mer fristende å klikk enn å tenke.

Det du vil oppdage hvis du prøver deg litt fram er at du av og til må gå imot en tilsynelatende opplagt plan. F.eks. kan en vinkel se ut til å være svært nære 90 grader. Det kan imidlerid tenkes at kostnaden med 90-graders løsningen må forkastes fordi gevinsten ved å vende de 2 andre i retning av 270 grader er større.

// Vi bestemmer oss for om vi skal
// gå for 90 eller 270 grader (targetVinkel)
// og hvor mange klikk det krever (sumKlikk)
function analyse(){
  sumKlikk=0;
  
  // 90 graders rotasjoner
  var roterTil90=0;
  for(var ix=1; ix <4 ;ix++)
    roterTil90+=til90(vinkel[ix]);
  
  // 270 graders rotasjoner
  var roterTil270=0;
  for(var ix=1; ix <4 ;ix++)
    roterTil270+=til270(vinkel[ix]);
  
  // hvem er mest effektiv
  if(roterTil90 < roterTil270){
    targetVinkel=90;
    sumKlikk=roterTil90/dv;
  }
  else{
    targetVinkel=270;
    sumKlikk=roterTil270/dv;
  }
}

// hvor mye må vi endre v
// for å få 90 grader
function til90(v){
  if(v < 90)   return 90-v;
  if(v < 180) return v-90;
  if(v < 270) return 90+v-180;
  return 90+(360-v);
}

// hvor mye må vi endre v
// for å få 270 grader
function til270(v){
  if(v < 90)   return 90+v;
  if(v < 180) return 270-v;
  if(v < 270) return 270-v;
  return v-270;
}

Når denne jobben er gjort kan vi fylle inn "minimium" -teksten øverst til høyre på tegneflaten.

Animasjon

Hvis vi velger å gjøre en animasjon går vi systematisk gjennom alle de tre siste vinklene og endrer dem til 90 eller 270.

// simuler et klikk i animasjonen
// targetVinkel er bestemt til 90 eller 270
function oneStep(){
  // rekkefølgen spiller ingen rolle
  for(ix=3; ix>0; ix--){
    var v=vinkel[ix];
    if(v!=targetVinkel){
      if(targetVinkel==90){
        if(( v < 90)||(v > 270))
          vinkel[ix]=v+dv;
        else
          vinkel[ix]=v-dv;
      }else{// targetVinkel==270
        if(v==0)
          vinkel[ix]=360-dv;
        else if((v<90)||(v>270))
          vinkel[ix]=v-dv;
        else
          vinkel[ix]=v+dv;
      }
      // hvis vi passerer 360
      vinkel[ix]=vinkel[ix] % 360;
      antallKlikk++;
      // bestill neste klikk om noen millisekunder
      setTimeout(oneStep, 200);
      return
    }
  }
}

Hvis du betrakter koden over i detalj, vil du kanskje se at det er mange måter å gå fram på. Det lar seg nok gjøre å lage koden mer kompakt, men tidsmessig er det ikke så mye å hente med å optimalisere, siden vi har så små tall.