Koordinat-mapping
Modellen og skjermen
Det ville være for snevert dersom vi måtte beskrive alle våre modeller i skjermkoordinater. Det vil ha flere ulemper:
- Vi ville kunstig måtte transformere modellen vår, enten den opprinnelig var beskrevet i mm eller km, til punkter.
- Vi måtte lage kode som hele tiden undersøkte og tok hensyn til den aktuelle skjermen.
- Vi ville være tvunget til å operere i heltallskoordinater, og vi ville utsette oss for akkumulerte avrundingsfeil.
Vi ønsker å kombinere maksimal frihet i modellbeskrivelsen med en fleksibel mapping til de til enhver tid aktuelle skjermkoordinatene.
I tradisjonell grafisk databehandling er det en tradisjon for å kalle modellkoordinatene World Coordinate System (wc) eller Logical Coordinate System (lc) og skjermkoordinatsystemet for Device Coordinate System (dc).
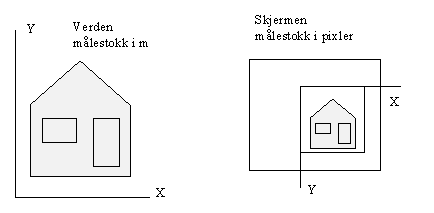
Når vi skal framstille noe på skjermen ønsker vi å avgrense både den delen av verden vi vil betrakte og den delen av skjermen som skal benyttes.
I grafisk databehandling er navnebruken litt forvirrende siden den delen av verden vi betrakter blir kalt Window, mens den delen av skjermen vi benytter kalles Viewport. årsaken til dette er at terminologien grafisk databehandling er eldre enn de vindussystemene vi kjenner i dag.
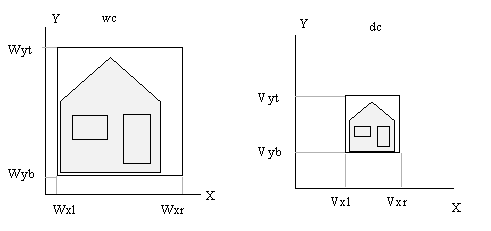
Vi spesifiserer altså Window i wc og Viewport i dc.
La oss anta at Window er spesifisert ved Wxl,Wxr,Wyt,Wyb og Viewport ved Vxl,Vxr,Vyb,Vyt.
En mapping av punktet P(xw,yw) i wc til P(xv,yv) i dc er da beskrevet i hht følgende:

![]() og
og
![]()
som gir oss
![]()
og
![]()
Vi kan skrive ut disse slik at vi ser at de inneholder både en skalerings- og en translasjonsfaktor:
xv=sx(xw-Wxl)+Vxl
og
yv=sy(yw-Wyb)+Vyb
Hvis vi betrakter (xw-Wxl) og (yw-Wyb) som koordinater relativt til origo i Window, ser vi at dette også lar seg formulere som en matrise.
Dersom utsnittet vi betrakter innebærer at deler av figuren faller utenfor innbærer avbildningen også klipping. Vi forfølger ikke dette her. Den mest vanlige klippealgoritmen for linjer er Cohen-Sutherlands klippealgoritme som er beskrevet i de fleste elementære bøker i grafisk databehandling.
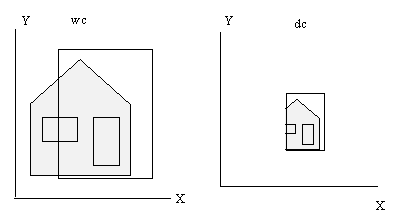
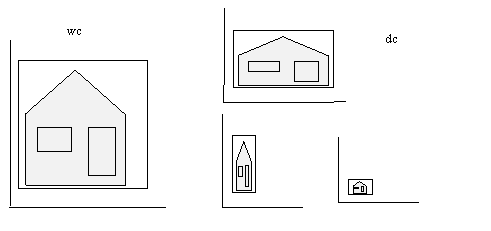
Vi ser lett at mappingen fra wc til dc kan være en måte både å zoome og fordreie på. Vi kan også flytte Window for å oppnå panorering.
MS Windows
Alle grafiske vindussystemer med respekt for seg selv har rutiner for å mappe verden til skjermen, slik også med MS Windows. MS Windows opererer med begrepene Logical Coordinates for modell-koordinater og Device Coordinates for skjerm-koordinater (og printer/plotter koordinater). MS Windows forutsetter dessuten at også de logiske koordinatene er beskrevet som heltall. Vi refererer hele tiden til det aktuelle vinduet, ikke hele skjermen. Funksjonsbatteriet er slik:
| SetWindowOrg | Setter origo i vinduet, logiske koordinater |
| SetWindowExt | Setter utstrekningen i vinduet, logiske koordinater |
| SetViewportOrg | Setter origo i viewport, device koordinater |
| SetViewportExt | Setter utstrekningen i viewport, device koordinater |
| LPtoD | Tar et enkeltpunkt fra modell til skjerm |
| DPtoLP | Tar et enkeltpunkt fra skjerm til modell. Nyttig ved tolkning av museinput inn i en modell |
| SetMappingMode | Angir typen av mapping. |
I Visual C++ er rutinene knyttet til MFC-klassen som representerer Device Context, CDC. Den siste rutinen, SetMappingMode, er interessant. Den gir oss en masse muligheter for å sette føringer på mappingen. F.eks. kan vi angi at mappingen skal være lik langs begge aksene, slik at vi ikke får forvrengninger. Vi kan også spesifisere mappingen slik at f.eks. et rutenett beskrives med fast størrelse, f.eks. 1 cm på både printer og skjerm. (Dette forutsetter at driverne er gode og nøyaktige). Se beskrivelsen av Windows eller MFC for en nærmere detaljer.
I eksempelprogrammet planalg.zip (se ref) benyttes en enkel mapping og programmet viser hvordan mappingen kan brukes til å regne, f.eks. teste innside, i logiske koordinater eller skjermkoordinater
Java
...kommer snart






