Eksamen mai 2001
|
21. mai 2001, kl 0900 - 1400 Alle skrevne og trykte hjelpemidler tillatt. Dersom du finner noe uklart i oppgaveteksten så gjør dine egne forutsetninger og redegjør for disse. Programskissene i besvarelsene nedenfor er skrevet i VC++. |

|
Det spiller ingen rolle om du skriver for C/Glut, VC++/MFC eller Java/Magician.
Oppgave 1 (30%)
Denne oppgaven etterspør noen matematiske formuleringer og vurderinger. Det fordres ikke programmering.
For enkelhets skyld tenker vi oss at vi opererer i planet, 2D
Oppgave 1a

|
Anta at vi har en rettstilt (normal)font beskrevet som linjer. Vi ønsker å lage skråstilt (italic) tekst som danner en vinkel V med vertikal-aksen. Lag en transformasjonsmatrise som foretar en slik skråstilling. |
Oppgave 1b
|
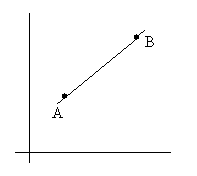
Hvis hvordan du vil bygge opp en transformasjonsmatrise som foretar en speiling om en akse gjennom A og B. Forklar og illustrer resonnementet steg for steg. |
Hva blir den endelige matrisa dersom A har koordinater (1,2) og B har koordinater (3,4) ?
Oppgave 1c
Du skal finne en parametrisk kurve av 3.grad som er bestemt ved følgende:
- den starter i P(2,4)
- den ender i Q(6,12)
når parameteren t løper fra 0 til 1.
- Tangentvektoren i P er (1,2)
- Tangentvektoren i Q er (1,-2)
Oppgave 2 (30%)
Denne oppgaven kan besvares rent teoretisk (matematisk), i pseudokode, i OpenGL kode eller ved en blanding. Velg det du synes får fram løsningen best.
Anta en sylinder med høyde H og diameter D.
Anta en kontinuerlig funksjon y=f(x). Beskriv hvordan du vil projisere denne funksjonen på sylinderens overflate. La x løpe langs sylinderens omkrets og y langs sylinderens høyde. Du skal tegne funksjonen i området fra x=xmin til x=xmax. Du kan forutsette at det finnes en funksjon f som tar x som input og som returnerer en y-verdi i området [ymin,ymax].
Angi kort, uten å gjennomføre detaljregning eller programmering, hvordan resonnementet må endres dersom du skal projisere på en kuleflate.
Oppgave 3 (30%)
Denne oppgaven skal besvares med relativt detaljert pseudokode, OpenGL-kode eller en kombinasjon.

|
Et firma har etablert en meget fleksible produksjonskjede for spiraltrapper, eller vindeltrapper. En trapp består av to typer elementer:
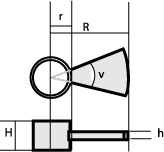
Et slikt trinnelement består av en ring som tres på sylinderen og et utstikk som er selve trinnet, se figuren nedenfor. |
Firmaet vil tilby kunden et system der en trapp kan tegnes ut etter gitte spesifikasjoner.
|
Lag en rutine som tegner ut en trapp, der følgende er gitt:
|
Du trenger ikke bekymre deg om hvordan disse verdiene spesifiseres, og du kan konsentrere deg om selve uttegningen. Du kan gjøre egne rimelige forutsetninger i tillegg til de som er listet ovenfor. Skriv ned eventuelle slike forutsetninger.
Oppgave 4 (10%)
Angi og begrunn kort noen av de virkemidlene vi kan bruke for å redusere forsinkelser i et OpenGL-program. Se bort fra maskinvare.
Forslag til løsning
Et program som dekker det meste er: solution.zip






