Litt algebra

Matriser

Addisjon

Vi vet at vi kan addere to matriser, eller to vektorer, dersom antall rader og antall kolonner er like i begge.

	A=B+C

	aij=bij+cij

alle rader i og kolonner j

Multiplikasjon

Vi vet at vi kan multiplisere to matriser dersom antall kolonner i den første matrisen er lik antall rader i den andre (n). Resultatmatrisen får like mange rader, nr, som den første matrisen og like mange kolonner, nk, som den andre.

	A=B*C

	for(r=1;r<=nr; r++)
	for(k=1;k<=nk; k++)
	{
		ar,k=sum(br,i*ci,k)
		i=1..n
	}

Transponering

Vi kan transponere matriser. Å transponere en matrise betyr rent teknisk å speile den om diagonalen. Diagonalen er de elementene med 2 like indekser. Vi skriver MT for den transponerte til matrisen M.

|m11 m12 m13 m14|T  |m11 m21 m31 m41|
|m21 m22 m23 m24| = |m12 m22 m32 m42|
|m31 m32 m33 m34|   |m13 m23 m33 m43|
|m41 m42 m43 m44|   |m14 m24 m34 m44|

Den transponerte til en radvektor P er en tilsvarende kolonnevektor.

             |x|
|x y z 1|T = |y|
             |z|
             |1|

Vi minner om modulene om transformasjoner i planet og rommet. Ved inspeksjon ser vi at matrisene vi benytter i uttrykkene P2=M·P1 er de transponerte av de vi benytter i uttrykkene P2=P1·M

Invertering

Den inverse av en matrise er definert ved at B sies å være den inverse av A dersom A·B=I, identitetsmatrisen. Geometrisk oppfatter vi dette slik at en matrise er invers av en annen dersom den opphever en transformasjon, dvs. gjør det motsatte. I enkle tilfeller kan vi resonnere oss fram til den inverse av en matrise på grunnlag av geometriske betraktninger. F.eks. kan vi anta at den inverse matrisen til en rotasjon om z-aksen med vinkelen v er en matrise med rotasjonen -v.

         |cos(v)  sin(v) 0 0|
R1=R(v)= |-sin(v) cos(v) 0 0|
         |0       0      1 0|
         |0       0      0 1|

         |cos(-v)  sin(-v) 0 0| |cos(v)  -sin(v) 0 0|
R2=R(-v)=|-sin(-v) cos(-v) 0 0|=|sin(v)   cos(v) 0 0|
         |0        0       1 0| |0        0      1 0|
         |0        0       0 1| |0        0      0 1|


         |cos(v)  sin(v) 0 0| |cos(v)  -sin(v) 0 0|
R1*R2=   |-sin(v) cos(v) 0 0|*|sin(v)   cos(v) 0 0|
         |0       0      1 0| |0        0      1 0|
         |0       0      0 1| |0        0      0 1|


         |cos^2(v)+sin^2(v)   0            0 0|
     =   |0              cos^2(v)+sin^2(v) 0 0|=I
         |0                 0            1 0|
         |0                 0            0 1|

siden

cos2(v)+sin2(v)=1

for alle v.

Dersom vi gir avkall på geometrisk kunnskap om matrisene må vi bruke standard algoritmer for å finne den inverse av en matrise. Vi forfølger ikke dette her, men slike algoritmer finnes i de fleste numeriske biblioteker.

Grafiske pakker har av og til bruk for å operere med inverse transformasjoner. Et slikt tilfelle er der vi interaktivt peker på en del av en figur og ønsker å finne hvilket objekt vi har pekt på. Vi ønsker da å inverstransformere de ulike objektene i figuren slik at de kan sammenlignes med pekepunktet.

I MS-Windows rutinebibliotek er det rutinene LPtoDP (Logical Point to Device Point) og DPtoLP (Device Point to Logical Point) som handterer transformasjoner mellom modellkoordinater og skjermkoordinater. Her er både modell- og skjerm- (device)koordinater gitt i planet.

Vi skal se i modulen: Å identifisere ved å peke at OpenGL benytter en annen strategi for å identifisere påpekte objekter i en tredimensjonal modell.

Vektorer

Lengden av en vektor

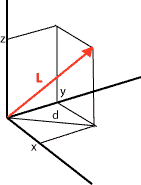
Anta en vektor A. Lengden til A i n-rommet er definert som

Dette er en ren generalisering av Pytagoras. For n=3, rommet, kan vi illustrere dette slik:

Skalarproduktet

Skalarproduktet av to vektorer er et tall, en skalar. Anta to vektorer A og B. Skalarproduktet er definert som

der n er dimensjonen til vektorene.

Vi setter n=3 og beskriver vektorene A og B som radvektorer: A=(2,3,5) og B=(1,-6,2). Skalarproduktet blir : A·B=2·1-3·6+5·2=-6

Vi ser videre at

F.eks kan vi la A være beskrevet ved (x,y,z), og vi kan skrive

Vi kan gjøre et resonnement i planet for å finne en alternativ formulering for skalarproduktet. Vi betrakter to vektorer A og B.

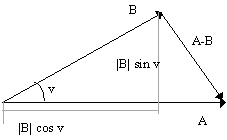
Vi kan skrive:

      |A-B|2
      =(|A|-|B|cos(v))2+|B|2sin2(v)
      =|A|2+|B|2cos2(v)-2|A||B|cos(v)+|B|2sin2(v)
      =|A|2+|B|2(cos2(v)+sin2(v))-2|A||B|cos(v)
      =|A|2+|B|2-2|A||B|cos(v)
    

Vi kan også skrive:

      |A-B|2
      =(A-B)(A-B)
      =AA-2AB+BB
      =|A|2+|B|2-2AB
    

Tilsammen gir dette oss:

      |A|2+|B|2-2AB=|A|2+|B|22|A||B|cos(v)
      AB=|A||B|cos(v)
    

Dette er interessant og nyttig fordi det sier oss at dersom vi kjenner to vektorer, kan vi finne cosinus til vinkelen mellom dem.

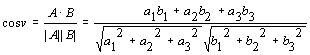
og dersom vektorene er normaliserte, har lengde 1, så kan vi skrive.

      cos(v)=AB.
    

I OpenGL benyttes vinkelen mellom ulike retninger (vektorer) hyppig, blant annet ved beregning av reflektert lys. For å få OpenGL til å oppføre seg fornuftig må vi av og til oppgi normalvektorer til flater vi spesifiserer:

  glNormal3f(x,y,z)

Internt vil OpenGL gjerne regne med disse som normaliserte vektorer. Vi kan unngå håndarbeidet med å normalisere vektorer ved å skru på automatisk normalisering:

  glEnable(GL_NORMALIZE)
   

Kryssproduktet

Kryssproduktet av to vektorer er en vektor, AxB=C. Vektoren C står vinklerett på A og B og har en retning slik at vektorene A,B og C danner et høyrehåndssystem. C er normalen til planet som er beskrevet ved A og B.

Kryssproduktet for to vektorer i rommet er definert som:

C=AxB=(a2b3-a3b2,
    a3b1-a1b3, a1b2-a2b1)
    

Dette har vi nytte av i situasjoner der vi skal spesifisere normaler til flater. Vi vet at dersom vi kjenner tre punkter (som ikke ligger på linje) i et plan kan vi beregne normalen til planet.

• Kilde for dette stoffet er bøker i algebra.
• De viktigste delene er, som her, summarisk behandlet i de fleste bøker i grafisk databehandling.
• Mer om matriser og litt til: The Matrix and Quaternions FAQ