Homogenisering av koordinater

Når vi innførte homogene koordinater var det for at vi skulle kunne multiplisere likeartede matriser for på den måten å oppnå den kombinerte geometriske effekten. I rommet fant vi fram til følgende sentrale 4x4 matriser:

1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1    

1 0 0 tx
0 1 0 ty
0 0 1 tz
0 0 0 1     

sx 0 0 0
0 sy 0 0
0 0 sz 0
0 0  0 1    

cos -sin 0 0
sin cos  0 0
0   0    1 0
0   0    0 1    

cos  0 sin  0
0    1  0   0
-sin 0 cos  0
0    0  0   1    

1 0     0   0
0 cos  -sin 0
0 sin  cos  0
0  0    0   1    

Det er normalt disse matrisene vi bruker når vi setter opp transformasjoner i modellene våre. Selv om rotasjonskommandoen i OpenGL er generalisert og kopler vinkel og rotasjonsakse, så er resultatet en kombinasjon av matrisene ovenfor.

Felles for alle disse matrisene og de matrisene vi får ved å multiplisere dem er at de har formen:

|a11  a12  a13  a14 |
|a21  a22  a23  a24 |
|a31  a32  a33  a34 |
| 0     0    0    W |    

der W alltid har verdien 1.

Hva dersom vi lager en matrise der W er forskjellig fra 1?

I enkelte sammenhenger er det nyttig å beregne en egen matrise og bruke denne direkte enten ved å sette den som OpenGLs aktuelle transformasjonsmatrise eller ved å multiplisere den til den aktuelle transformasjonsmatrisa. OpenGL har kommandoer for å gjøre begge disse operasjonene:

   glLoadMatrixd(...)
   glMultMatrixd(...)
 

Når OpenGL transformerer et punkt skjer det alltid en "homogenisering" av resultatet. Det betyr at koordinatverdiene divideres med W. Vi ser på en translasjon som eksempel:

        |1 0 0 a| |x| |x+a|
P'=M*P =|0 1 0 b|*|y|=|y+b|
        |0 0 1 c| |z| |z+c|
        |0 0 0 W| |1| |W  |
 

og homogenisert:

|(x+a)/W|
|(y+b)/W|
|(z+c)/W|
|1      |
 

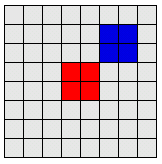De 2 kodebitene (GL4Java syntaks) nedenfor produserer begge samme figur:

drawSquare(red);
gl.glTranslated(2.0,2.0,0.0);
drawSquare(blue);

drawSquare(red);
double M_mult[]={
2.0,  0.0,  0.0,  0.0,
0.0,  2.0,  0.0,  0.0,
0.0,  0.0,  2.0,  0.0,
4.0,  4.0,  0.0,  2.0
};
gl.glMultMatrixd(M_mult);
drawSquare(blue);

Merk transponeringen av matrisen i forhold til oppsettet ovenfor.