de Casteljau kurver

Hva

En alternativ måte å betrakte Bezier kurver

Vi kan komme fram til Bezier-kurven på en helt annen måte, via de Casteljau-algoritmen.

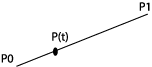
Utgangspunktet er den parametriske formen på en linje som skal være slik at P(0)=P0 og P(1)=P1: P(t)=(1-t)P0+tP1. Et resonnement etter de Casteljaus algoritme fører til at dette kan oppfattes som et spesialtilfelle av en Bezier-kurve, en lineær Bezier-kurve.

Algoritmen kan beskrives etter følgende skjema, der vi hele tiden tenker oss at t løper fra 0 til 1:

  P(t)=(1-t)P0+tP1

  P(t)=(1-t)A(t)+tB(t)

og:

  A(t)=(1-t)P0+tP1
  B(t)=(1-t)P1+tP2

Vi setter inn og får:

  P(t)=(1-t)²P0+2t(1-t)P1+t²P2

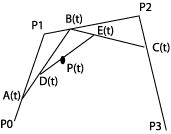
  P(t)=(1-t)D(t)+tE(t)

og:

  D(t)=(1-t)A(t)+tB(t)

  E(t)=(1-t)B(t)+tC(t)

og:

  A(t)=(1-t)P0+tP1

  B(t)=(1-t)P1+tP2

  C(t)=(1-t)P2+tP3

Vi setter inn i to omganger og får:

 P(t)=(1-t)³P0+3t(1-t)²P1+3t²(1-t)P2+t³P3

Det siste uttrykket er det samme som det vi kom fram til ovenfor, når vi tok utgangspunkt i et generelt tredjegradspolynom og føringer på endepunktene og den deriverte i endepunktene.

Det er lett å overbevise seg om at vi kan gjenta de Castelajau-algoritmen med ytterligere styrepunkter, P4, P5 etc.

Du kan eksperimentere nedenfor.

Flytt kontrollpunktene og drag teksten nederst med musa