MathML

Det har tradisjonelt vært et problem å framstille matematiske uttrykk på vevsider. En måte å løse dette på er som følger:

1. Åpne MS Word eller Open Office Writer og lag et nytt dokument
2. Sett inn et objekt av type Equation på siden, og rediger formelen ved hjelp av Equation Editor
3. Frys dokumentet, klipp ut bildet og lim det inn i vevsiden.

Et alternativ er slik:

1. Åpne MS Word og lag et nytt dokument
2. Sett inn et objekt av type Equation på siden, rediger formelen ved hjelp av Equation Editor
3. Spar dokumentet som html, formelen blir lagret som gif i en subkatalog som kalles images.
4. Plukk opp det riktige bildet og lim det inn i vevsiden

... og vi kan få Taylors formel slik:

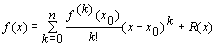
Dette er ikke noen god løsning. Dels gjør vi oss avhengig av Equation editor, dels er det stor sannsynlighet for at dokumentet med tilhørende formler forsvinner, dels har vi ingen mulighet til å endre stil eller størrelse av noe slag når bildet først er laget og dels tar slike bilder av formler stor plass.

Enkle uttrykk som involverer eksponenter og indekser kan vi få til i vanlig HTML, ved hjelp av elementene <sup> og <sub>. F.eks slik:

X²+Y²=R²

   X<sup>2</sup>+Y<sup>2</sup>=R<sup>2</sup>

Y:{w₁,v₃,}

   Y:{w<sub>1</sub>,v<sub>3</sub>}

Dette gir oss alt for lite spillerom til å formulere matematisk uttrykk.

MathML

MathML gjør det mulig for oss å editere matematikken direkt på siden. Eller vi kan bruke en WYSIWYG editor eller vi kan bruke Equation Editor i Open Office som genererer MathML-kode. I slutten av denne modulen finner du en oppskrift på hvordan vi kan benytte oss av dette.

Eksempel 1

Vi lager en enkel kvadratrot med summen av to kvadrater.

<math style="font-weigth:bold;
      font-size:18px">
   <mi>r</mi>
   <mo>=</mo>
   <msqrt>
      <mrow>
         <mo>(</mo>
         <msup>
            <mi>x</mi>
            <mn>2</mn>
         </msup>
         <mo>+</mo>
         <msup>
            <mi>y</mi>
            <mn>2</mn>
         </msup>
         <mo>)</mo>
      </mrow>
   </msqrt>
</math>

Eksempel 2

Vi lager en 3X3 matrise (som framstiller en rotasjonstransformasjon i planet).

<math style="font-weigth:bold;
      font-size:18px">
<mrow>
  <mi>R</mi>
  <mo>=</mo>
  <mfenced open="[" close="]">
    <mtable>
      <mtr>
         <mtd>
            <mi>-cos</mi>
            <mo>
            (</mo>
            <mi>v</mi><mo>)
            </mo>
         </mtd>
         <mtd>
            <mi>sin</mi>
            <mo>
            (</mo><mi>v</mi><mo>)
            </mo>
         </mtd>
         <mtd>
            <mi>0</mi>
         </mtd>
      </mtr>
      <mtr>
         <mtd>
            <mi>sin</mi>
            <mo>
            (</mo><mi>v</mi><mo>)
            </mo>
         </mtd>
         <mtd>
            <mi>cos</mi>
            <mo>(</mo><mi>v</mi><mo>)
            </mo>
         </mtd>
         <mtd>
            <mi>0</mi>
         </mtd>
      </mtr>
      <mtr>
         <mtd><mi>0</mi></mtd>
         <mtd><mi>0</mi></mtd>
         <mtd><mi>1</mi></mtd>
      </mtr>
    </mtable>
  </mfenced>
</mrow>
</math>

Eksempel 3

<math style="font-weigth:bold;
      font-size:18px">
    <mrow>
      <mi>B</mi>
      <mrow>
        <mrow>
          <mo stretchy="false">(</mo>
          <mi>t</mi>
          <mo stretchy="false">)</mo>
        </mrow>
        <mo stretchy="false">=</mo>
        <mrow>
          <munderover>
            <mo stretchy="false">∑</mo>
            <mrow>
              <mi>i</mi>
              <mo stretchy="false">=</mo>
              <mn>0</mn>
            </mrow>
            <mi>n</mi>
          </munderover>
          <msubsup>
            <mi>B</mi>
            <mi>i</mi>
            <mi>n</mi>
          </msubsup>
        </mrow>
      </mrow>
      <mrow>
        <msup>
          <mi>t</mi>
          <mi>i</mi>
        </msup>
        <msup>
          <mrow>
            <mo stretchy="false">(</mo>
            <mrow>
              <mn>1</mn>
              <mo stretchy="false">−</mo>
              <mi>t</mi>
            </mrow>
            <mo stretchy="false">)</mo>
          </mrow>
          <mrow>
            <mo stretchy="false">(</mo>
            <mrow>
              <mi>n</mi>
              <mo stretchy="false">−</mo>
              <mi>i</mi>
            </mrow>
            <mo stretchy="false">)</mo>
          </mrow>
        </msup>
        <msub>
          <mi>P</mi>
          <mi>i</mi>
        </msub>
      </mrow>
    </mrow>
</math>

Editere MathMl

Det finnes en del MathML-editorer på nettet dersom du tar et søk. Det finnes dessuten en litt involvert måte å editere formler på ved hjelp av Open Office:

1. Opprett et tekstdokument i Open Office, sett inn et object av type equation og editer denne.
2. Spar dokumentet, f.eks. som minfil.odt.
3. Siden .odt formatet egentlig er et .zip format kan vi døpe om fila til minfil.zip og pakke den ut, i Windows ganske enkelt ved å dobbeltklikke. Vi finner da en katalogstruktur. Fila content.xml beskriver strukturen i fila vår. Subkatalogene objectn, der n er en fortløpende indexering, inneholder beskrivelser av objekter i dokumentet. En av disse objektene er den formelen vi leter etter.
4. Hver av objektene inneholder en content.xml fil. For vår formel er dette en formelbeskrivelse i MathML. Plukk denne opp i en editor.

Litt tungvindt, men kan forenkles en god del dersom du har en zip-følsom applikasjon. Netbeans er et alternativ hvis du arbeider med dette verktøyet i andre sammenhenger. Netbeans betrakter minfil.odt som en katalog og åpner denne direkte. (fordi .odt, .zip og .jar i prinsipp er samme format og NetBeans kjenner jar-formatet og er programmert til åpne det)