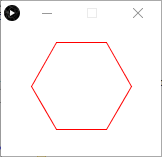
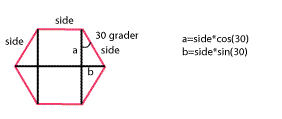Vi skal tegne en sekskant på to forskjellige måter. Begge gir dette resultatet:
De to metodene representerer etter min erfaring en ganske typisk situasjon når vi programmerer i slik grafiske omgivelser.
Den første metoden er ganske intiutiv og vi finner på en måte veien rent algoritmisk.
Den andre metoden er basert på et matematisk, geometrisk resonnemet.
Metode1
Skissen er slik:
//En regulær sekskant (hexagon)
float side=50.0;
void setup(){
size(160,130);
noLoop();
}
void draw(){
background(255);
translate(30,60);
drawSekskant();
}
void drawSekskant(){
pushMatrix();
stroke(0,0,255);
rotate(-TWO_PI/12);
for(int i=0; i< 6;i++){
line(0,0, 0,side);
translate(0,side);
rotate(-TWO_PI/6);
}
popMatrix();
}
Det vi har gjort her, drawSekskant(), er rett og slett at vi har dratt med oss en strek i en vandring rundt sekskanten.
Vi går seks steg, hver med en lengde lik sidekanten, og vi snur oss 6o grader i hvert hjørne (60*6=360).
Vi kan på en måte si at i har tegnet en ufullstendig sirkel. Hvis vi øker antall steg og reduserer vinkelen i hvert hjørne tilsvarende
kan dette bli slik:
Skissen som lager dette er slik:
// likesidede mangekanter
float side;
void setup(){
side=35.0;
size(500,500);
noLoop();
}
void draw(){
background(255);
stroke(0,0,255);
translate(side,200);
for(int ix=3;ix<40;ix++)
drawPolygon(ix);
}
void drawPolygon(int n){
pushMatrix();
for(int i=0; i< n;i++){
line(0,0, 0,side);
translate(0,side);
rotate(-TWO_PI/n);
}
popMatrix();
}
Metode2
Her tar vi utgangspunkt i en analyse av dimensjonene i et hexagon:
Skissen regner ut a og b ved hjelp av sinus og cosinus og er slik:
float side=50.0;
void setup(){
size(160,130);
noLoop();
}
void draw(){
background(255);
translate(30,60);
drawSekskant();
}
void drawSekskant(){
PShape sekskant;
float a=side*cos(TWO_PI/12);// 30 grader
float b=side*sin(TWO_PI/12);
sekskant = createShape();
sekskant.beginShape();
sekskant.stroke(255,0,0);
sekskant.vertex(0 ,0);
sekskant.vertex(b ,-a);
sekskant.vertex(side+b ,-a);
sekskant.vertex(side+2*b ,0);
sekskant.vertex(side+b ,a);
sekskant.vertex(b ,a);
sekskant.endShape(CLOSE);
shape(sekskant);
}
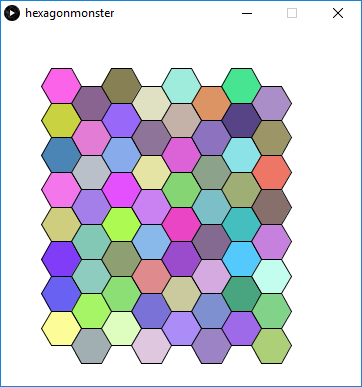
Hexagonmønster
Vi skal ordne et antall hexagoner i et sammenhengende mønster. Vi lager noe slikt:
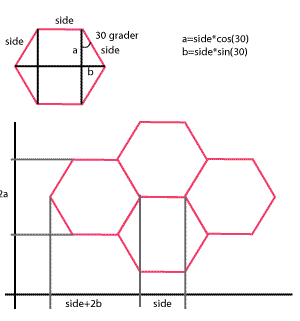
Her må vi forholde oss til hexagonenes forhold til hverandre. Det er vel ganske klart at metode1 ovenfor er
det beste utgangspunktet. Vi kan ressonere ut fra følgende plan:
Vi ordner oss slik at hvert hexagon beskrives med et objekt. Når vi klikker på det skrur vi av og på synligheten:
class hexagon{
float xPos;
float yPos;
color col;
PShape hShape;
boolean synlig;
hexagon(float xPos,float yPos, color col){
this.xPos = xPos;
this.yPos = yPos;
this.col = col;
this.synlig=true;
this.hShape=createShape();
this.hShape.beginShape();
this.hShape.fill(this.col);
this.hShape.vertex(0,0);
this.hShape.vertex(b,-a);
this.hShape.vertex(side+b,-a);
this.hShape.vertex(2*side,0);
this.hShape.vertex(side+b,a);
this.hShape.vertex(b,a);
this.hShape.endShape(CLOSE);
}
void tegn(){
if(!this.synlig)
return;
pushMatrix();
translate(this.xPos,this.yPos);
shape(this.hShape);
popMatrix();
}
boolean truffet(){
float centerX=this.xPos+side/2+b;
float centerY=this.yPos;
// omtrentlig
if( dist(mouseX,mouseY,centerX,centerY) < side){
this.synlig=!this.synlig;
return true;
}
return false;
}
}
Selve skissen er slik:
//flere sekskanter
float side,a,b;
ArrayList<hexagon> ruter;
void setup(){
size(360,360);
side=20.0;
a=side*cos(TWO_PI/12);
b=side*sin(TWO_PI/12);
setupRuter();
}
void draw(){
background(255);
for(int i=0;i < ruter.size();i++)
ruter.get(i).tegn();
}
void setupRuter(){
ruter=new ArrayList<hexagon>();
float top=60;
for(int r=1;r<8;r=r+2)
for(int i=0;i< 8;i++){
// ulike farger
color c1=color(random(60,255),random(60,255),random(60,255));
color c2=color(random(60,255),random(60,255),random(60,255));
// her setter vi posisjonene
ruter.add(new hexagon(10+r*(side+b), top+i*2*a, c1));
ruter.add(new hexagon(10+(r+1)*(side+b),top+a+i*2*a, c2));
}
}
void mousePressed(){
for(int i=0; i< ruter.size();i++){
if(ruter.get(i).truffet()){
return;
}
}
}
Oppgaverforslag
Alternative plasseringer
Lage en skisse som legger ut hexagoner i et annet mønster
Avsløring
Legg et bilde bak exagonene og la brukeren finne ut hva/hvem bildet representerer
med færrest mulig klikk på hexagoner (som kan skrus av og på).
Eller la hexagonene skru seg tilfeldig av og på helt til brukeren kjenner igjen bildet.
Dessuten
Visste du forresten at fotballer ofte sys sammen av 2 0hexagoner og 12 pentagoner (5-kanter):