Glatting av terrengflater i 3D

Hva

Når man skal glatte flater i 3 dimensjoner så kan det gjøres på flere forskjellige måter, man bygger gjerne videre på glattings algoritmer som brukes på bilder altså 2 dimensjoner. For å få glattet flater så må de kjøres igjennom ett filter, ett filter er en algoritme som på en eller annen måte behandler høydeverdiene i flaten slik at de blir jevnere og glattere enn de var. Filtrene fungerer forskjellig basert på hvordan glatting man vil foreta, noen filtre baserer seg på nabopunktene i ett visst område når ett punkt skal filtreres. Andre filtre bruker avanserte matematiske metoder for å beregne en filtrert punktverdi. For å kunne gi en innføring i filter/glattingsalgoritmer må vi se på ett par grunnprinsipper hos filtre før beskrivelsene av de filterenes som er implementert her blir beskrevet.

De algoritmene som blir beskrevet er:

Båndfilter
Lavpassfilter
Høypassfilter
Gjennomsnittfilter
Kuwaharafilter
Gaussfilter

Terreng modellering i 3D er mye brukt i spill og i simulatorer og skal helst virke så naturlig som mulig for å oppnå størst mulig realisme. Terreng modellering baserer seg på gjerne på høydefelt som er en matrise i 3 dimensjoner med x, y og z koordinater, der z er høydeverdiene. Det finnes flere måter å beskrive terreng på men det er høydefelt som er i fokus i denne modulen. Når et slikt høydefelt skal tegnes ut på skjermen bruker man gjerne triangler, størrelsen på trianglene spiller en stor rolle i hvor glatt terrenget virker, jo mindre triangler jo glattere virker overflaten. Det er som oftest ikke nok å tegne opp ett terreng med små triangler for å få en glatt overflate, det må gjerne kjøres glattings algoritmer på høydefeltet for å legge høydepunktene(z verdiene) nærmere hverandre. Det er disse algoritmene for glatting av høydefelt som utforskes nærmere i denne modulen.

Filter

Filter er en type algoritmer som siler dataene som kommer inn på en eller annen måte. Det finnes flere typer filter for å fjerne eller fremheve spesielle egenskaper ved inn dataene. I dette tilfellet så siler filtrene ut høydeverdier som på en eller annen måte utmerker seg, det kan være at de er unormalt høye iforhold til sine naboverdier eller unormalt lave iforhold til sine naboer. På denne måten oppnår vi at filteret glatter høydefeltet slik at det blir mindre kantete og ujevnt.

Vinduer

Mange glattingsalgoritmer benytter seg av det som kalles vinduer/kjerner. Det som skjer ved bruk av vinduer er at selve høydefeltet blir delt opp i ett antall vinduer, der vinduet har en viss størrelse som er mindre enn selve høydefeltet. Dette gjøres slik at hele høydefeltet tilslutt er dekket av forskjellige vinduer, vinduene kan overlappe hverandre eller de kan ligge kant i kant. Det finnes mange forskjellige måter å distribuere vinduer utover ett høydefelt.

kernel_4_example
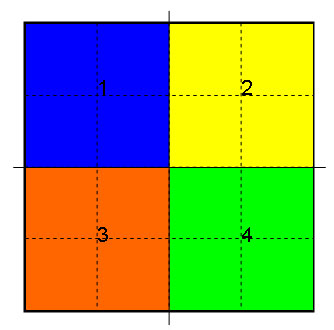
Figur 1

Figur 1 illustrerer hvordan ett høydefelt på størrelse 5x5 punkter deles opp i 4 vinduer, nummereringen i figuren forteller hvilket vindu som er plassert hvor, altså er vindu 1 øverste venstre del av høydefeltet. Det er oppdeling av ett høydefelt i fire vinduer som er det mest vanlige og den enkleste måten å gjøre dette på.

kernel_9_example
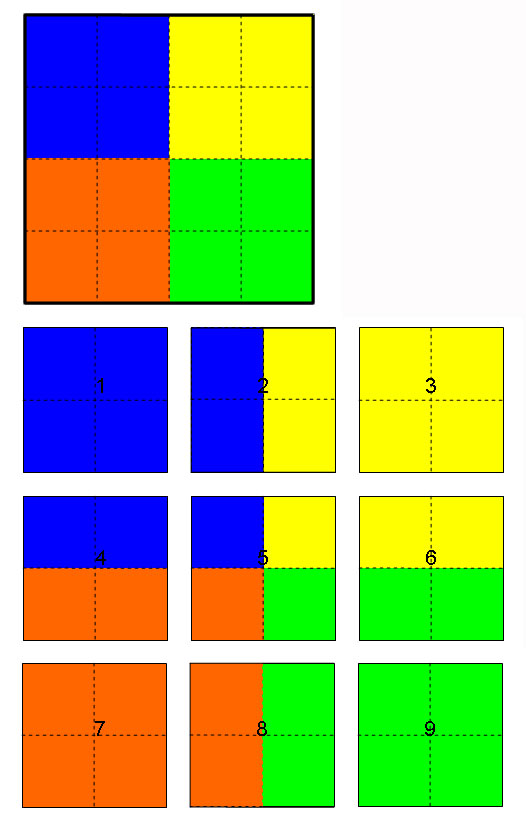
Figur 2

Figur 2 viser en annen måte å bruke vinduer i ett høydefelt på, her brukes det ni vinduer på hele høydefeltet. Her overlapper alle vinduene hverandre, slik at de deler opptil flere punkter samtidig. Dette er en måte å som sikrer at høydeverdiene blir mest mulig korrekte i forhold til sine naboverdier.

Konvolusjon

Konvolusjon er en generisk måte å definere filter på. Den bruker modifiserer høydefeltet ved bruk av vinduer, og/eller en annen konstant. Vinduene brukes som beskrevet ovenfor, og innen hvert vindu blir konstanten brukt til å utføre en eller annen beregning, denne beregningen kan skje på alle høydeverdiene i vinduet eller på noen utvalgte høydeverdier. Vindusstørrelsen i en konvolusjon er gjerne ujevne tall, oddetall. Av de filterene som er implementert her, bruker gjennomsnittsfilteret og kuwaharafilteret konvolusjon, men de fleste filtrene kunne blitt implementert basert på konvolusjon.

Bånd filter

Båndfilter er muligens ett av de enkleste filtrene for å glatte ett høydefelt, hovedprinsippet i et båndfilter er å ta en rad eller kolonne i høydefeltet og glatte denne. Den nye verdien til punktet baseres på den opprinnelige høydeverdien til punktet, høydeverdien til nabopunktet og en konstant som settes før filteret kjøres. Konstanten kalt k i denne implementasjonen strekker seg fra 1.0 til 0.0, jo mindre k er jo glattere skal terrenget bli. Utregningen nedenfor beskriver båndfilteret når det kjøres på x aksen fra venstre til høyre.

matrix[x][y][2] = (matrix[x - 1][y][2] *(1-k)) + (matrix[x][y][2] * k);

I denne implementasjonen av båndfilter kjøres det først glatting på x aksen fra høyre til venstre, så fra venstre til høyre. Når det er gjort kjøres det en glatting på y aksen, først ovenfra og ned, for så å glatte nedenfra og opp.

private void rightSmooth(int x, int y, float k){
  if(x == 0)
    return;
  matrix[x][y][2] = (matrix[x - 1][y][2] *(1-k)) + (matrix[x][y][2] * k);
  rightSmooth(x - 1, y, k);
}

Figur 3

Implementasjonen av båndfilter er gjort rekursivt, når glattingen blir kalt så kjøres det en for løkke som løper igjennom størrelsen på høydefeltet, for hver iterasjon blir det kalt opp rekursive metoder som kjører glatting på den aktuelle posisjonen i høydefeltet. I figur 3 så er den rekursive metoden for å glatte fra fra venstre til høyre, de andre rekursive metodene baserer seg på dette oppsettet.

bandfilter
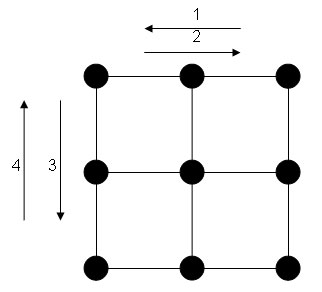
Figur 4

Figur 4, ovenfor viser hvordan filteret jobber 1. glatter fra høyre til venstre, 2. venstre til høyre. 3. ovenfra og ned 4. nedenfra og opp.

original_10
Figur 5

band_output_3it_02k
Figur 6

Figur 5 er det orginale høydefeltet uten noen glattinger, figur 6 er glattet med bandfilter 3 ganger og med konstant k på 0.2.

Lavpass filter

Lavpass filter kan implementeres på flere ulike måter, det finnes mange forskjellige sofistikerte måter å bygge opp dette på som baseres på de ulike egenskapene man vil ha frem ved ett terreng. I sin opprinnelige form og slik det er implementert i denne modulen så får selve filteret inn en parameter som definerer det høyeste "lovlige" høydeverdien. Alle høydeverdier som er over denne satte maksimal verdien blir byttet ut med denne maksimal verdien, de verdiene som er under den satte maksimum verdien blir ikke berørt på noen som helst måte. På denne måten favoriseres laveverdier og disse fremheves i motsetning til ett høypassfilter som favoriserer høye verdier.

lowpass_example
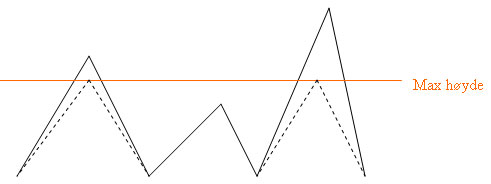
Figur 7

I figur 7 er de helstrukne linjene orginal høydeverdiene, den oransje linjen markerer høyeste lovlige høydeverdi. De stiplede linjene markerer hvordan de høydeverdiene med for høy verdi blir plassert etter at lavpassfilteret er brukt på høydefeltet.

for(int x = 0; x < getMatrixSize(); x++){
  for(int y = 0; y < getMatrixSize(); y++){
    if(matrix[x][y][2] > getParameter())
      matrix[x][y][2] = getParameter();
  }
}

Figur 8

Figur 8 viser hvordan lavpassfilteret går igjennom høydefeltet og bytter ut alle høydeverdiene som er høyere enn det som er definert i getParameter() med verdien i getParameter().

lowpass_1it_1f
Figur 9

Figur 9 er glattet med lavpassfilteret, der høyeste lovlige verdi er 1.0, det orginale høydefeltet er vist i figur 5.

Høypass filter

Høypass filter fungerer så og si på samme måte som ett lavpass filter, men i favoriserer høye høydeverdier isteden for lave høydeverdier. Det er også slik at ett høypass filter kan implementerer på forskjellige måter, siden denne modulen ser på glatting av terreng flater generelt så har dette filteret blitt implementert i sin orginale form. Dette vil si at filteret får inn en parameter, denne parameteren definerer den laveste "lovlige" høydeverdien, alle høydeverdier som er lavere enn denne minimum verdien blir byttet ut med minimum verdien, andre verdier blir ikke forandret.

highpass_example
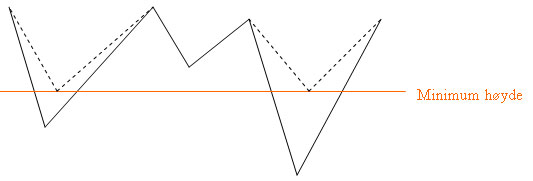
Figur 10

I figur 10 er de helstrukne linjene orginale høydeverdier, den oransje linjen definerer laveste lovlige høydeverdi. De stiplede linjene viser hvordan høydefeltets laveste verdier vil ha forandret seg etter at det er kjørt ett høypassfilter på høydefeltet.

for(int x = 0; x < getMatrixSize(); x++){
  for(int y = 0; y < getMatrixSize(); y++){
    if(matrix[x][y][2] < getParameter())
      matrix[x][y][2] = getParameter();
  }
}

Figur 11

Figur 11 beskriver hvordan høypassfilteret går igjennom høydefeltet, getParameter() inneholder laveste lovlige verdi i høydefeltet. Hvis verdien i høydefeltet sin x og y posisjon er mindre enn laveste lovlige verdi, så byttes verdien ut i høydefeltet sin posisjon x og y med laveste lovlige verdi.

highpass_1it_2f
Figur 12

Figur 12 viser høydefeltet når det er kjørt et høypassfilter med 2.0 som laveste lovlige verdi. Orginal høydefeltet er vist i figur 5.

Gjennomsnitt filter

Meanfilter eller gjennomsnittfilter som det også kalles, kalkulerer en punktverdi ved å se på nabopunktenes verdi. Dette skjer ved å finne de nærmeste naboene rundt punktet som skal utregnes, vanlig å bruke 3x3 eller 5x5 rutenett for å kartlegge naboene. Når nabopunktene er funnet så beregnes gjennomsnittet av alle disse punktene og punktet som skulle beregnes får den utregnede verdien.

Gjennomsnittfilter er mye brukt i bildebehandling for å fjerne støy i bilder, men det egner seg også godt til å glatte 3D flater.

Denne implementasjonen av mean filter bruker ett 3x3 vindu for å finne nabopunkter, når kantpunkter skal utregnes går det derimot ikke å bruke ett 3x3 vindu da de ikke har så mange naboer. Løsningen på det har blitt slik at hjørnepunkter danner sin verdi basert på 2x2 vindu, altså sine 3 nærmeste naboer og seg selv. andre kantpunkter bruker ett 3x2 vindu eller 2x3 vindu og finner sine 5 nærmeste naboer og seg selv.

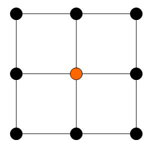Figur 13

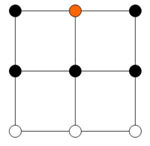Figur 14

Figur 15

I figurene over ser man hvordan utvelgingen av nabopunkter skjer utifra hvilke punkt som skal utregnes. Dette er basert på ett 3x3 vindu. De oransje punkene er punktene som skal få en ny verdi basert på naboverdiene, de svarte punktene er nabopunkter som blir brukt til å regne ut ny verdi til det oransje punktet. Figur 13 viser da hvordan senter punkter finner sine naboer, figur 14 viser hvordan kantpunkter finner sine naboer og tilslutt figur 15 viser hvordan ventre hjørne punkt finner sine naboer.

private float center(int x, int y){
  float average = 0.0f;
  x = x - 1;
  y = y - 1;

  for(int tx = x; tx <  x + KERNEL_SIZE; tx++){
    for(int ty = y; ty < y + KERNEL_SIZE; ty++)
      average += matrix[tx][ty][2];
  }
  return average / (KERNEL_SIZE * KERNEL_SIZE);
}

Figur 16

Koden i figur 16 viser hvordan gjennomsnittsfilteret beregner gjennomsnittet høydeverdier som har åtte naboer. KERNEL_SIZE er størrelsen på vinduet som legges rundt høydeverdiene, average variabelen holder på summen av alle høydeverdiene og deles på antall høydeverider i vinduet når verdien returneres fra metoden. Gjennomsnittsfilteret har fire private metoder som brukes i smooth metoden, den ene er beskrevet i figur 16, de tre andre er lignende metoder men som regner ut horisontale kantverdier, vertikale kantverdier og hjørneverdier.

mean_orginal
Figur 17

mean_2_iterations
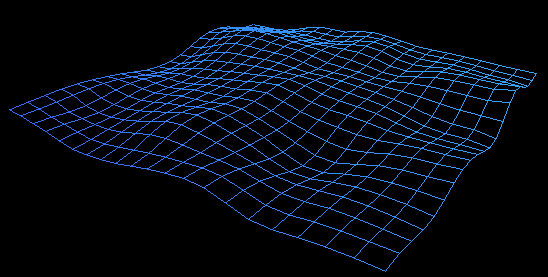
Figur 18

Figur 17 er det orginale høydefeltet, mens gjennomsnittfilteret har blitt kjørt to ganger på figur 18. Vi kan se at gjennomsnittsfilter er et godt filter for å glatte flater med, overflaten blir jevnere og det forandrer ikke høydefeltet for mye pr iterasjon som blir gjennomført på høydefeltet.

Kuwahara filter

Kuwaharafilter baserer seg på konvolusjon også kalt vinduer, som er beskrevet nærmere tidligere i modulen. Det finnes mange måter å implementere ett kuwaharafilter på, den implementasjonen som er gjort her baserer seg på flere forskjellige kilder/tolkninger av filteret. Hovedessensen i kuwaharafilteret er å splitte hele høydefeltet opp i flere vinduer, implementasjonen som er gjort her bruker 4 vinduer, som da inneholder 1/4 av høydefeltet hver. Hvert vindu beregner gjennomsnittet for hver høydeverdi, dette gjøres ved å bruke gjennomsnittsfilteret som er beskrevet ovenfor, deretter beregnes gjennomsnittsverdien av hele vinduet. Videre beregnes variansen for hver høydeverdi i vinduet ut, formelen for å beregne variansen av disse høydeverdiene er vist i figur 19.

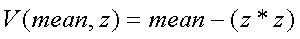
kuwahara_variance
Figur 19

Der mean er gjennomsnittsverdien til hele vinduet, og z er høydeverdien i den aktuelle x, y posisjonen i høydefeltet. Hele vinduet blir deretter tilegnet den samme høydeverdien som den høydeverdi med lavest varianse. Alt dette gjøres da i fire iterasjoner for å dekke alle fire vinduene. Noe av det viktigste med ett kuwahara filter er at det ikke kan brukes på alle typer høydefelt, det er kun høydefelt med en størrelse som er større en 5x5 punkter og høydefelt der størrelsen ikke er partall, det er som sagt kun høydefelt med størrelse lik oddetall som kan brukes. Dette er fordi at vinduene skal dele på nabopunktene. I figur 20, nedenfor ser du hvordan de forskjellige vinduene deler de forskjellige høydepunktene. Vindu 1 og vindu 2 deler de gule punktene, vindu 1 og 3 deler de blå punktene, vindu 2 og 4 deler de oransje punktene, vindu 2 og 4 deler de grønne punktene og alle vinduene deler det svarte punktet.

kuwahara_kernel_points
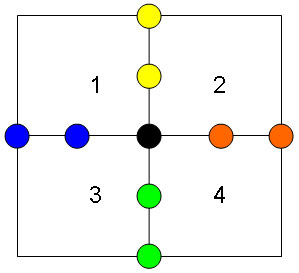
Figur 20

public void smooth(){
  //Bestemmer størrelsen på hvert vindu.
  kernel_size = (getMatrixSize() + 1) / 2;

  //Sjekker at størrelsen på vinduet er oddetall.
  if(correct_size){
    int tmpX = 0;
    int tmpY = 0;

    //Bruker 4 vinduer,
    for(int h = 0 ; h < kernels / 2; h++){
      for(int v = 0; v < kernels / 2; v++){

        //Henter alle verdiene til det aktuelle vinduet.
        float kernel[][][]  = getKernel(tmpX, tmpY);

        //Finner gjennomsnittet til vinduet.
        meanFilter.setMatrix(kernel);
        meanFilter.smooth();
        kernel = meanFilter.getMatrix();

        //Henter variansen til høydepunktene i vinduet.
        float var[][][] = kernelVariance(kernel, kernelMean(kernel));

        //Bytter ut de gamle høydeverdiene med de nye.
        kernel = replace(kernel, var);

        //Legger vinduet tilbake på plass i høydefeltet.
        insertNewValues(kernel, tmpX, tmpY);

        tmpX = kernel_size - 1;
      }
      tmpX = 0;
      tmpY = kernel_size - 1;
    }
  }
}

Figur 21

Figur 21 viser hvordan kuwaharafilteret bruker fire vinduer, hvordan hvert vindu beregner gjennomsnitt og varians, og tilslutt legger verdiene regnet ut i hvert vindu tilbake på plass i høydefeltet. Figur 22 viser det orginale høydefeltet før det er kjørt noe kuwaharafilter på terrenget. I figur 23 ser man hvordan ett høydefelt har blitt glattet med ett kuwaharafilter, man ser tydelig hvordan vinduene er plassert og at de gir samme verdi til alle høydepunktene i vinduet. Man ser også det man kan kalle terskeleffekten i høydefeltet, dette kommer av bruken av vinduer og deres deling av nabopunkter. Kuwaharafilter egner seg godt til å glatte flater for å få hele høyefeltet i samme høyde. Noe av det som trekker ned ved ett kuwaharafilter er at det ofte blir ett klart skille der vinduene har vært. Dette er noe som selfølgelig kan justeres ved å bruke mange og små vinduer, eller ved å bruke kuwaharafilteret på høydefeltet igjennom flere iterasjoner.

kuwahara_original
Figur 22

kuwahara_1_iteration
Figur 23

Gaussfilter

Gaussfilter har vist seg å bli ett populært filter spesielt innen bildebehandling men også innen behandling av 3d flater. Gaussfilter er fleksibelt på den måten at det kan brukes til forskjellige ting, det kan være å oppdage kanterpunkter i ett høydefelt, det kan være å fjerne støy i et bilde eller slik vi bruker det her, til å glatte flater. Gaussfilter bruker flere matematiske og statisktiske uttrykk for å beregne ny høydeverdi til alle høydepunktene. Det finnes flere måter å implementere ett gaussfilter på, både med og uten vinduer, implementasjonen av gaussfilter bruker noen antagelser x y og z i høydefeltet er stokastiske variabler, og de er normalfordelt der forventningsverdien my er 0. Når disse antagelsene er gjort kan man begynne å beregne gaussfilteret for x og y dimensjonene, formelen for å regne ut dette er beskrevet i figur 24. Siden det jobbes i tre dimensjoner må vi regne ut gaussfilteret for x og y dimensjonene dette gjøres ved først å regne ut dimensjonene hver for seg som vist i figur 24. Når dette er gjort multipliseres x og y dimensjonene sammen som vist i figur 25, denne formelen kan videre generaliseres slik at man får kun ett uttrykk som vist i figur 26. Det er formelen i figur 26, som er implementert i dette gaussfilteret.

Gaussian_formula
Figur 24

3D_gaussian_formula
Figur 25

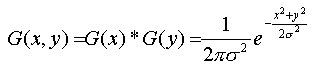
3D_gaussian_formula_new
Figur 26

Deretter kjøres det en laplace operasjon på gauss resultatet og hver av dimensjonene, formelen for dette er beskrevet i figur 27, siden deltaverdien i figuren multipliseres med resultatet fra gauss operasjonen vil forandringer i den påvirke glattingen. Jo lavere deltaverdien er jo mer glattes flaten. Resultatet av laplace operasjonen multipliseres med høydeverdien til x og y dimensjonene og blir den nye høydeverdien for høydepunktet, formelen for å regne ut høydeverdien v.h.a laplaceoperasjoen er beskrevet i figur 28, der Z høydeverdien til x og y.

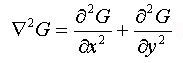
laplacian
Figur 27

height_calculation
Figur 28

public void smooth(){
  for(int x = 0; x < getMatrixSize(); x++){
    for(int y = 0; y < getMatrixSize(); y++){
      float gauss = gauss(matrix[x][y][0], matrix[x][y][1]);
      matrix[x][y][2] = laplace(gauss, matrix[x][y][0], matrix[x][y][1]) * matrix[x][y][2];
    }
  }
}

Figur 29

I figur 29, ovenfor, er noe av koden for å kjøre ett gaussfilter beskrevet, for løkkene kjører igjennom hele høydefeltet, det første som gjøres med ett punkt i høydefeltet er å beregne gaussverdien til x og y koordinatene, det er metoden gauss(matrix[x][y][0], matrix[x][y][1]) som gjør dette. Gauss metoden bruker formelen som er beskrevet i figur 26 for å gjøre dette. Når det er gjort beregnes laplaceverdien basert på den utregnede gaussverdien og x og y koordinatene, denne metoden bruker formelen beskrevet i figur 27. når denne verdien er funnet multipliseres laplaceverdien med høydeverdien i z koordinatet, og høydepunktet blir tildelt den nye verdien, altså laplaceverdien multiplisert med den orginale høydeverdien.

I figur 30, nedenfor illustrerer hvordan ett høydefeltet er blitt flatet v.h.a gaussfilteret, gaussfilteret er her kjørt med 1 iterasjon på høydefeltet. Orginalen av dette høydefeltet er vist i figur 22. Det som er mest innlysende når man ser på ett høydefelt som er glattet med ett gaussfilter er at det glatter veldig mye, det vil si at det tar ikke så godt vare på de høydeverdiene som var der orginalt. Dette kan jo selvsagt forandres noe ved å sette andre sigma og delta verdier. Sigma verdiene forandrer utfallet av formelen i figur 26, mens delta verdien forandrer utfallet av laplace formelen i figur 27. Det som også kan være noe problematisk ved gaussfilter er at det det krever endel datakraft, så glatting av store høydefelt kan ta noe tid.

Gaussian_1iteration
Figur 30

Høydefelt i openGL

For å lage og tegne ut høydefelt, har det blitt laget to hovedklasser for å jobbe med dette, HeightField klassen holder på høydefelt informasjonen, altså en tre dimensjonal array, med x, y, og z informasjon. Denne informasjonen brukes av TerrainCanvas, denne klassen har alt ansvar for å tegne ut høydefeltene. Alle metodene for å tegne ut høydefeltet er rekursive, metoden draw kaller to metoder drawTriangle og drawOppositeTriangle, disse står for å tegne ut hver sin motstående trekant av en firkant, som vist i figur 30 og figur 31. Dette må gjøres slik at alle kantpunktene skal kommer riktig med.

Figur 31

Figur 32

I figur 33 ser vi at både drawTriangle og drawOppositeTriangle metodene bruker gl.glVertex3f dette er en metode for å tegne ut tre dimensjonale punkter. Videre henter gl.glVertex3f sin informasjon om hvert punkt i høydefeltet fra heightField objektet. I draw metoden brukes gl.glBegin(GL_LINE_STRIP) og gl.glEnd() metodene disse tegner opp alle punktene(vertexene) som ligger inne i den blokken, GL_LINE_STRIP betyr at den bruker linjer mellom punktene(vertexene).

private void draw(int x, int y){
    if(x == 0)
      return;
    gl.glBegin(GL_LINE_STRIP);
      drawOppositeTriangle(x, y);
    gl.glEnd();
    gl.glBegin(GL_LINE_STRIP);
      drawTriangle(x, y);
    gl.glEnd();
    draw(x - 1, y);
  }

//Recursive method used by draw.
private void drawTriangle(int x, int y){
  if(y == 0) return;

  gl.glVertex3f(heightField.getWidth(x, y),
                heightField.getHeight(x, y),
                heightField.getLength(x, y));
  gl.glVertex3f(heightField.getWidth(x-1, y),
                heightField.getHeight(x-1, y),
                heightField.getLength(x-1, y));
  gl.glVertex3f(heightField.getWidth(x-1, y-1),
                heightField.getHeight(x-1, y-1),
                heightField.getLength(x-1, y-1));

  drawTriangle(x, y - 1);
}

//Recursive method used by draw.
private void drawOppositeTriangle(int x, int y){
  if(y == 0) return;

  gl.glVertex3f(heightField.getWidth(x, y),
                heightField.getHeight(x, y),
                heightField.getLength(x, y));
  gl.glVertex3f(heightField.getWidth(x, y-1),
                heightField.getHeight(x, y-1),
                heightField.getLength(x, y-1));
  gl.glVertex3f(heightField.getWidth(x-1, y-1),
                heightField.getHeight(x-1, y-1),
                heightField.getLength(x-1, y-1));

  drawOppositeTriangle(x, y -1);
}

Kode

Filter:

Filter.java
BandFilter.java
LowpassFilter.java
HighpassFilter.java
MeanFilter.java
KuwaharaFilter.java
GaussianFilter.java

TerrainViewer:

TerrainViewer.java
TerrainCanvas.java
TerrainLoader.java
HeightField.java
KeyManager.java
MouseManager.java
WindowManager.java
TerrainGenerator.java

Hele systemet zippet.

Referanser

Remote Sensing and Image Interpretation, fourth editionT. Lillesand,R. KieferWiley0-471-25515-7

Principles of Geographical Information SystemsPeter A Burrough,Rachael A. McDonnellWiley0-19-823365-5

MATHEMASteffen LogTapir Akademisk Forlag8251919398

Innføring i Sannsynlighetsregning og StatistikkPer Chr. HagenCappelen82-02-19887-9

Smoothing OperationsTUDelftwww.ph.tn.tudelft.nl/Courses/FIP/noframes/fip-Smoothin.html14-04-2010

Digital FiltersUniversity of Edinburghhomepages.inf.ed.ac.uk/rbf/HIPR2/filtops.htm14-04-2010