Figurer og flater

Basis i OpenGL

De grunnleggende mekanismene for å skape flater i OpenGL er enkle. Hvis vi skjærer alt ned til beinet er det grunnleggende, og prinsippielt eneste, tegneprimitivet:

glVertex(x,y,z)

Vi kan ved hjelp av en rekke parametre sette OpenGL i tilstander som tolker sekvenser av vertex-kall på ulike måter. Først og framst kan vi ramme inn slike sekvenser av glVertex-kall på en slik måte at vi kan tegne polygoner av ulik art, f.eks.:

glBegin(GL_POLYGON)
  glVertex(x1,y1,z1)
  glVertex(x2,y2,z2)
  glVertex(x3,y3,z3)
  ...
  glVertex(xn,yn,zn)
glEnd()

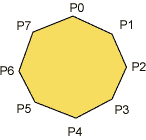
Parameteren i glBegin() bestemmer hvordan en sekvens av glVertex-kall skal tolkes:

GL_POINTS	GL_POLYGON	GL_QUADS
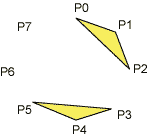
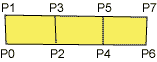
GL_TRIANGLES	GL_TRIANGLE_STRIP	GL_QUAD_STRIP

OpenGL kan kun handtere konvekse polygoner på en sikker måte. Årsaken til dette er er at konvvekse polygoner er lette å handtere i en dybdekø når vi skal avgjøre hva som skal være synlig og hva som skal skjules. Flatene kan sorteres entydig i avstand fra betrakteren. Dette er mer komplisert og ressurskrevende dersom flatene er konkave, se figuren. Det er lov å spesifisere konkave polygoner, men resultatet er ikke garantert.

Vi vet videre at polygoner med mer enn tre hjørner kan være buet i den forstand at polygonet ikke nødvendigvis ligger i et plan.

Quadricer

OpenGL har et batteri med hjelperutiner som tegner "standarfigurer" (quadricer) som er plassert i glu-delen av biblioteket. Figurene er kule, sylinder og skive. Vi kan bestemme en rekke egenskaper ved disse standardfunksjonene, både ved parametre i selve funksjonskallet og ved å sette opp tilstandsparametre. Noen eksempler med tilhørende kode:

glShadeModel(GL_SMOOTH); gluSphere(qd,2.0,15,15);	glShadeModel(GL_FLAT); gluSphere(qd,2.0,15,15);
glShadeModel(GL_SMOOTH); gluCylinder(qd,2.0,2.0,2.5,15,15);	glShadeModel(GL_FLAT); gluCylinder(qd,2.0,2.0,2.5,15,15);
glShadeModel(GL_SMOOTH); gluCylinder(qd,2.0,0.0,2.5,15,15);	glShadeModel(GL_SMOOTH); gluDisk(qd,1.0,2.0,15,15);
gluQuadricDrawStyle(qd,GLU_LINE); gluSphere(qd,2.0,10,10);	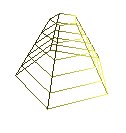gluQuadricDrawStyle(qd,GLU_LINE); gluCylinder(qd,2.0,0.5,2.5,5,5);

Vi kan kombinere slike standardfigurer, og med litt kreativitet er det mye det går an å lage med disse.

Generelle datastrukturer

OpenGL er kun et rutinebibliotek og har ikke definert noe dataformat for geometriske beskrivelser. Det hadde vært ønskelig å kunne flytte modellbeskrivelser fra 3D-tegneprogrammer til OpenGL-programmer på en enkel og fleksibel måte. Vi kunne kanskje ønske oss et sett rutiner av typen loadFigurFromFile() og renderFigur(). Det er selvsagt ikke noe i veien for at vi lager slike hjelperutiner selv med den fleksibiliteten vi måtte ønske. Det vil medføre en rekke problemer å gjøre dette generelt. Siden OpenGL er en tilstandsmaskin så ville tegnerutinene måtte forutsette, eller sette, de nødvendige tilstandsparametrene. Vi må vite om flatene er generert med eller mot klokka, vi må ta hensyn til om både front og bak skal genereres, om vi skal ha fylte flater osv.

Det finnes en rekke mer eller mindre standardiserte formater for transport av 3D-figurer. Noen av dem har sitt opphav i bestemte produkter og/eller spesielle anvendelsesområder og noen av dem er forsøk på generelle standarder. Blandt de siste er VRML (X3D).

Det er nok riktig å betrakte OpenGL som et grunnleggende tegnebibliotek som kan brukes til å bygge applikasjoner som kan handtere ulike typer data.

Hvis vi skulle nærme oss dette problemet er det nærliggende å se hva vi kunne få til med de enklest mulige flatene, trekanter. Alle flater burde kunne la seg beskrive som trekanter, og de har som bemerket ovenfor den egenskapen at de har samme normal i all punkter. Det betyr at normalene lett kan beregnes fra trekantens hjørner. Følgende er utsnitt fra et datasett som beskriver en figur laget i 3DStudio. Datastrukturen er bygd opp av trekanter. De første linjene viser hvilke hjørner som inngår i trekantene og de siste linjene viser koordinatene til hjørnene:

  indexes to trianglecorners
  0, 13, 12,
  0, 1, 13,
  1, 14, 13,
  1, 2, 14,
  ...
  286, 11, 10,
  286, 287, 11,
  287, 0, 11,
  287, 276, 0

  corners
  69.3 5.89 0,
  63.4 16.1 0,
  53.2 22 0,
  41.5 22 0,
  ...
  34.7 -19.7 -9.31,
  45.7 -22.8 -12.3,
  56.7 -19.7 -15.2,
  64.8 -11.4 -17.4

Dataene ovenfor er i VRML-format, og er flater tatt fra følgende figur:

Du kan se datafila i sin helhet her torus_wrl.html. Du kan jo se om du ser hvordan du kunne lage en rutine som ekstraherer det nødvedige for å gjenskape figuren med OpenGL-kall. Du kan kjøre den i en plugin som viser VRML i nettleseren direkt torus.wrl, hvis du har en slik installert.

Databasert

Ofte får vi data fra målinger. Typisk er at vi ha koordinatfestede høyder. 3D-kart er eksempel, enten det nå er fra havbunnen, jordoverflaten eller fra seismiske målinger. Andre eksempler er koordinatfetede målinger eller tellinger av ymse slag (nedbør, folketetthet, luftforurensning eller hva du nå kan finne på). Felles for slike data er at de ofte må bearbeides før de skal framstilles. De må kanskje glattes eller filtreres på en eller annen måte og de skal ofte fargekodes.

Modulen Skygge og glatting tar for seg noen enkle fltreringsmetoder. Figurene nedenfor er hentet derfra og viser en flate før og etter en slik filtrering.

Funksjoner

Vi kan lete etter matematiske funksjoner som framstiller flater i rommet. Funksjoner som typisk vil ha formen z=f(x,y). Tegningen nedenfor viser en flate som er generert som en grovmasket (nxn, n=10) sinus:

	f(x,y)=h·sin(pi·x/n)sin(pi ·y/n).
	

Selv om dette kanskje kan tjene som en hette fra middelalderen, vil vi fort finne at det ikke er lett å finne generelle funksjoner som lar seg uttrykke som z=f(x,y) og som passer til vårt formål, hva nå det måtte være.

Det som er fruktbart er å lage flater basert på polynomer på parametrisk form, av typen:

	x(t)=fx(t)
	y(t)=fy(t)
	z(t)=fz(t)
	

Ved å la t løpe over et område i (små) steg kan vi beregne x,y og z-verdier. Funksjonene f er polynomer, og vi kan bestemme koeffisientene i polynomene ved å sette opp noen grensebetingelser. Dette er behandlet i modulen Parametrisk formog i modulen Polynomer.

Bezierflater og NURBer som er vist nedenfor er basert på et slikt prinsipp.

Bezier

Bezierflater ( se modulen Bezier) er en enkel og rask måte å beskrive flater på. Figuren nedenfor er fra modulen Trampoline og viser en symmetrisk bezierflate med linjer mellom de 16 kontrollpunkter.

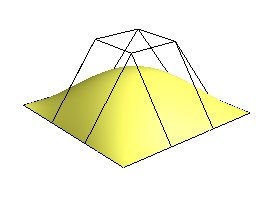
Bezierflater kan beskrives med mange kontrollpunkter, men det kan fort bli numerisk usikkert når antallet øker. Bezierflater kan også skjøtes slik at skjøtene blir så glatte som vi ønsker oss. Dersom vi vil arbeide med omfattende flater er NURBer å foretrekke, se nedenfor.

NURB

Non Uniform Rational B-splines ( se modulen NURB) er en mer fleksible metode for å beskrive flater enn Bezierflater. Vi kan beskrive større flater og vi kan kontrollere kontinuiteten i flaten, glattheten, på en enklere måte enn ved skjøtede Bezier-flater. Figuren nedenfor er fra modellering av vannoverflate som er beskrevet i modulen Vannflate. Figuren viser kontrollpunktene til en flate.

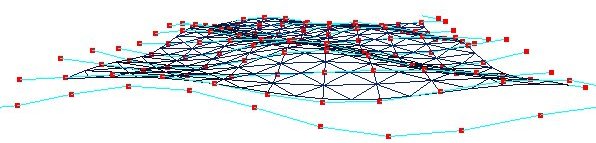
Noen teknikker

Rotasjon

Vi kan beskriver figurer ved å rotere konturer rundt en akse. På illustrasjonen nedenfor er kunturen beskrevet med en Bezierfunksjon med 4 kontrollpunkter i xz-planet. Konturen er rotert rundt z-aksen.

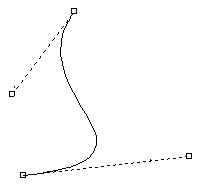
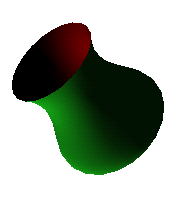
Ekstrudering

Ekstrudering er det samme uttrykket som brukes i produksjonsprosesser der vi f.eks. ekstruderer rør, det vil si at vi klemmer materiale ut av en form i en bestemt retning. Vi kan tenke oss å beskriver en kontur og trekker konturen i en retning. Illustrasjonen endenfor viser en Bezier-kontur i xy-planet som er "ekstrudert" langs z-aksen.

Sveiping

En teknikk vi kan bruke er en slags morfing. Det vil si at vi kan beskrive to sett med endepunkter for en flatekontur og la programmet beskrive alle mellomliggende konturer.

Konturene kan være rette linjer eller polynomer av høyere orden. Vi kan f.eks. bruke Bezierkurver som konturer.

Vending

Når vi skal framstille symmetriske figurer vil vi ofte kunne nøye oss med å framstille den ene halvparten, vende koordinatsystemet 180 grader og tegne en gang til.

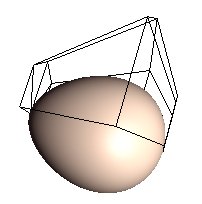En eggform er umulig å beskrive ved hjelp av en standard quadric og det er laget en bezierflate for halvparten av egget. Figuren viser et egg som er laget ved å tegne et halvt egg to ganger. Kontrollpunktene er tegnet ut for den ene halvparten.

Klippeplan

Et nyttig hjelpemiddel er midlertidige klippeplan. Vi kan sette opp plan som skjærer vekk en del av en form.

Hvis vi ønsker å hakke hodet av det egget vi tegnet ovenfor kan vi gjøre det ved å sette et klippeplan. Figuren er laget ved å tegne samme halv-egg 4 ganger.

Tekanna

En klassiker i grafisk databehandling er "The Utah Teapot". Hvis du vil vite mer om denne så se her: https://sjbaker.org/teapot/. Her er referanser til forskjellige kilder og du kan finne det komplette datasettet. Tekanna er dessuten tatt med som glut-funksjon i distribusjonen av GL4Java.