Slagskygge

Skygger er en svært viktig egenskap for vår oppfattelse av verden. Det hjelper oss å bedømme et objekts form og egenskap, samt at det er en avgjørende faktor for å avgjøre dybde og avstand til det vi ser. Selv om vi kanskje ikke tenker så mye over hva skygger egentlig betyr for vår oppfattelse av omgivelsene, vil vi umiddelbart merke at en 3D scene uten skygger mangler liv og realisme. Derfor er beregning av skygge et svært viktig virkemiddel for å skape en troverdig kopi av "den virkelige verden" i 3D grafikk.

Da jeg startet arbeidet med denne modulen trodde jeg at det skulle være lett å finne mye stoff om et så tilsynelatende sentralt emne i 3D grafikk. Det ligger riktignok en del programeksempler på Internett, men disse er ofte dårlig kommentert og løsningene på skyggeproblemet er properitære. Derfor har mye av arbeidet med denne modulen bestått i å samle og lese teoretisk materiale om skyggekasting i OpenGL. Like viktig som programeksemplene jeg har laget til emnet, føler jeg at denne modulen er. Jeg har forsøkt å samle informasjon om forskjellige angrepsmåter, og gi en oversikt over disse på denne siden. Jeg har forsøkt å lage den nettsiden jeg selv kunne tenkt meg å lese da jeg startet med denne arbeidsoppgaven.

Viktig forkunnskap

Det kan være nødvendig å ha en del grunnelggende kunnskap innenfor OpenGL før man gir seg i kast med slagskygge i denne modulen. Disse modulene er nyttige:
Teksturer, 2D transf., 3D transf., Plan

Ellers finner man mye nyttig i boken: "OpenGL Programming Guide, Third Edition av Woo, Neider, Davis og Shreiner". Særlig nyttig for utvikling av denne modulen har disse kapitlene vært:
Kapittel 6: Blending, Antialiasing, Fog and Polygon Offset
Kapittel 9: Texture Mapping
Kapittel 10: The Framebuffer

I tillegg har jeg måttet finne mye dokumentasjon om emnet på egenhånd.

Tre hovedstrategier for slagskygge i OpenGL

Skygger er som tidliger nevnt et viktig virkemiddel for å skape realisme i en tredimensjonal scene. Men som med flere andre ting i OpenGL må vi ta hensyn til konflikten mellom kvalitet/realisme og ytelse. Det er viktig med en grunnleggende forståelse for hvilken rolle lyset spiller ved skyggekasting. Det er derfor en fordel å ta for seg lys i OpenGL før man gir seg i kast med beregninger av skygger. Akkurat som med lys har vi mulighte til økende nivåer i realisme når det gjelder skygge, men dette går ofte på bekostning av ytelsen ved rendering av en scene.

OpenGL støtter ikke slagskygge direkte, men det er flere måter å implementere skyggefunksjoner med det eksisterende biblioteket. Disse metodene varierer i vansklighetsgrad ved implementasjon, og kvalitet av resultat. Vi kan si at kvaliteten til en skygge varierer som en funksjon med to parametre. Kompleksiteten til objektet som skal kaste skygge og kompleksiteten til objektet som blir skyggelagt.

Det er tre hovedstrategier for å lage slagskygge i OpenGL, projeksjons-skygger (Projection Shadows), skyggevolum (Shadow Volumes) og skyggekart (Shadow Maps). Innenfor disse tre strategiene er igjen flere detaljeringsnivåer alt etter hvor avansert kunnskap man har om OpenGL.

Projeksjons-skygger

Projeksjons-skygger, Projection Shadows, er en enkel måte å implementere skygge på i en OpenGL scene. Et objekt er ganske enkelt projisert på et plan, for så å rendres som et separat objekt.

Jeg vil ta for meg et svært enkelt eksempel på en slik projeksjons-skygge. Vi tenker oss at vi har et plan, en trekant og en lyskilde.

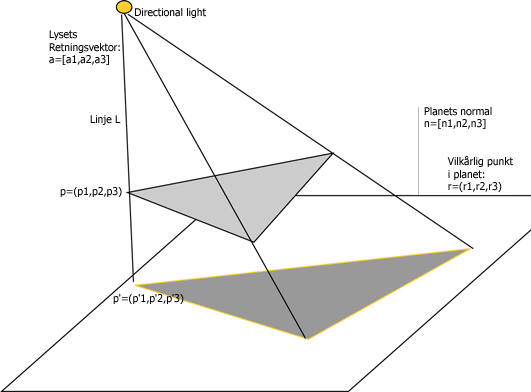
Når trekanten ligger mellom planet og lyskilden vil vi få en slagskygge på planet. Spørsmålet er da hvordan vi skal finne form og plassering av skyggen på planet. Vi tenker oss vektorer som går fra lyskilden, gjennom hjørnepunktene på trekanten og som fortsetter til de skjærer planet. For å finne hvilket punkt disse vektorene skjærer planet må vi ha noen forutsetninger på plass.

En linje L gjennom et punkt p = (p1,p2,p3) og med samme
retning som a = [a1,a2,a3] er samlingen av alle
punkter x på formen: x = p + t*a.
Dette gir oss for x1,x2 og x3:
(1)   x1 = p1 + t*a1
      x2 = p2 + t*a2
      x3 = p3 + t*a3

Likning for et plan er gitt ved:
(2)   n1*r1 + n2*r2 + n3*r3 + d = 0
      hvor planets normal n = [n1,n2,n3]
      og et vilkårlig punkt i planet r = (r1,r2,r3).

For å finne punktet på linje L som ligger i planet
har vi sammenhengen:
(3)   n1(p1 + t*a1) + n2(p2 + t*a2) + n3(p3 + t*a3)=
      n1*r1 + n2*r2 + n3*r3

Vi finner t:
(4)   n1*p1 + n1*t*a1 + n2*p2 + n2*t*a2 + n3*p3 + n3*t*a3 =
      n1*r1 + n2*r2 + n3*r3

      n1*t*a1 + n2*t*a2 + n3*t*a3 =
      n1*r1 + n2*r2 + n3*r3 - n1*p1 - n2*p2 - n3*p3

      t(n1*a1 + n2*a2 + n3*a3) =
      n1(r1 - p1) + n2(r2 - p2) + n3(r3 - p3)

      t = (n1(r1 - p1) + n2(r2 - p2) + n3(r3 - p3))/
      (n1*a1 + n2*a2 + n3*a3)

Vi kan nå sette inn t i likningsettet (1) for
å finne x1,x2 og x3.

Dette er altså koordinatene for et punkt i planet på rett linje L som gjennomløper punktet p (objektet som skal kaste skygge)og som har en retningsvektor a (lysets retning)

Dette beyr at for å finne skyggen som en trekant kaster på et plan må vi ha følgende: Punktene som skal projiseres på planet. Retningsvektor til lyset. Hvis lyset er "uendelig langt borte (direction) vil alle vektorene til lyset være parallelle når de treffer et objekt. Vi har da kun et punkt (f.eks p1) og lysets retningsvektor. Hvis derimot lyset har en eksakt plassering (positional) vil hver vektor fra lyset gjennom et punkt ha forskjellig retning. Vi må da regne ut retningsvektoren for hver linje L som gjennomløper punktene i trekanten og skjærer planet. I programeksempelet mitt har jeg tatt utgangspunkt i et directional lys. Vi må også ha likningen til planet slik at vi kan finne hvor i rommet linjen L skjærer planet.

Screenshot fra simpleshadow.java

Koden til simpleshadow.java: simpleshadow.java
Textur brukt til programmet kan du se her: marblefloor.png

I programmet har jeg brukt disse metodene for beregning av normal til plan og selveste projeksjonen:

//Finner normalen til et plan basert på tre kjente punkter i planet
public float[] calculateNormal(float p1[],float p2[],float p3[])
{
   float normal[] = new float[3];

   //Calculate the normal vector for the plane
   //Gitt to vektorer (tre punkter) i planet kan normalen regnes
   //ut.

   normal[0] =
   (((p2[1]-p1[1])*(p3[2]-p1[2]))-((p2[2]-p1[2])*(p3[1]-p1[1])));

   normal[1] =
   (((p2[2]-p1[2])*(p3[0]-p1[0]))-((p2[0]-p1[0])*(p3[2]-p1[2])));

   normal[2] =
   (((p2[0]-p1[0])*(p3[1]-p1[1]))-((p2[1]-p1[1])*(p3[0]-p1[0])));

   return normal;
}

//Metode som regner ut parameter t ut  fra et gitt punkt på en gitt
//flate og med retningsvektor lik lysets retning. r er et gitt punkt
//i planet, p er punktet som skal projiseres, n er planets normal og
//a er lysets retningsvektor.

public float[] calculateProjection(float r[], float p[], float n[],
   float a[]){

   float projection [] = new float[3];

   //Regner ut t
   float t =
   (n[0]*(r[0] - p[0]) + n[1]*(r[1] - p[1]) + n[2]*(r[2] - p[2]))/
   (n[0]*a[0] + n[1]*a[1] + n[2]*a[2]);

   //Setter t inn i likningsettet (1)
   float x1 = p[0] + (t * a[0]);
   float x2 = p[1] + (t * a[1]);
   float x3 = p[2] + (t * a[2]);

   projection[0] = x1;
   projection[1] = x2;
   projection[2] = x3;

   return projection;
}

Rendrer så projeksjonspunktene som et nytt objekt med ønsket farge og egenskaper for skygge. For å unngå "stitching" bruker jeg polygon offset som er forholdsvis godt dokumentert i koden.

Kommentarer til simpleshadow.java

Jeg hadde ingen erfaring med programmering med OpenGL da dette kurset startet. For å få en følelse av matematikken og de forskjellige beregningene som ligger bak blant annet transformasjoner i OpenGL, valgte jeg å gå grunnleggende til verks i dette programmet. Jeg har derfor ikke benyttet de muligheten som er implementert i OpenGL med hensyn til "Viewing og Modelling Transformations" og matrisemultiplikasjon ("glMultMatrixf(...)"). Jeg har implementert de metodene jeg har trengt selv for å få en større forståelse av det som skjer. Koden kan derfor virke litt tung ettersom jeg ikke har brukt en del av de innebygde metodene i OpenGL.

Fordeler og ulemper med projeksjons-skygger

Denne metoden å skape skygger på er begrenset av flere faktorer. For det første er det vanskelig å bruke denne angrepsmåten når vi har behov for å kaste skygge på mer komplekse objekter enn flater. Det er mulig å projisere på et objekt oppbygd av polygoner ved å finne hvert polygons planlikning for så å "klippe" skyggen i henhold til polygonenes grenser. Av og til kan Depth buffering benyttes til dette. Når vi har en modell som kun består av gulv og vegger som i simpleshadow, er denne metoden akseptabel.

Et annet problem med denne metoden er å kontrollere fargen til skyggen. Ettersom skyggen er en "sammenklemt" versjon av objektet som kaster skygge, vil normalene til skyggen bli påvirket. Dette får konsekvenser for lyssetting og andre egenskaper ved skyggen.

Ettersom jeg i simpleshadow ikke direkte projiserte skyggen ved hjelp av matrisemultiplikasjon har jeg unngått det siste. Skyggen er et selvstendig objekt regnet ut med hensyn til de regler som gjelder for projeksjon. Normalene til skyggen er ikke blitt manipulert, og jeg kan derfor sette ønsket materialegenskaper på den. Det neste eksempelt hvor jeg bruker matrisemultiplikasjon vil derimot inneholde dette problemet.

Projeksjons-skygger med Stencil

I programmet simpleshadow brukte jeg en tilnærming til projeksjons-skygge hvor jeg styrte alle translasjoner og rotasjoner selv for å kunne holde på de forskjellige koordinatene til trekanten. Men man kan enklere oppnå den samme effekten ved å bruke en kjent algoritme for projeksjoner på plan. Denne algoritmen er lett å implementere og passer til alle tilfeller hvor et objekt skal kaste skygge på et kjent plan.

Skyggematrise (Shadow matrix)

Gitt likningen til et plan og posisjonen til lyset, kan man konstruere en 4x4 skyggematrise (planar projected shadow matrix). Denne projiserer 3D polygoner til et spesifisert grunnplan basert på lysets posisjon. Ved å tranformere et polygonalt objekt med skyggematrisen, blir alle objektets polygoner "stablet" på grunnplanet slik at det danner en skyggeeffekt. Man kan tenke på denne skyggen som en "haug" med projiserte polygoner uten høyde.

Vi må altså lage en skyggematrise for så å multiplisere denne med modelview matrisen. Skyggen blir så gitt farge og vindus koordinater (rasterized) og lagt på grunnplanet ved ganske enkelt og rendre objektet en gang til.

Algoritmen for skyggematrisen er godt kjent. Min implementasjon av denne ser slik ut:

//Funksjonen returnerer en 4x4 skygge matrise gitt to arrayer som
//inneholder planlikningen for plan som skygge skal kastes på og
//lysets posisjon
public float[] shadowMatrix( float plane[], float light_pos[]) {
       float shadow_mat[] = new float[16];
       float dot;

       //Finner dot produktet mellom lysvektor og planets normal
       dot = plane[0] * light_pos[0] +
        plane[1] * light_pos[1] +
        plane[2] * light_pos[2] +
        plane[3] * light_pos[3];

       shadow_mat[0] = dot - light_pos[0] * plane[0];
       shadow_mat[4] = -light_pos[0] * plane[1];
       shadow_mat[8]  = -light_pos[0] * plane[2];
       shadow_mat[12] = -light_pos[0] * plane[3];

       shadow_mat[1]  = -light_pos[1] * plane[0];
       shadow_mat[5]  = dot - light_pos[1] * plane[1];
       shadow_mat[9]  = -light_pos[1] * plane[2];
       shadow_mat[13] = -light_pos[1] * plane[3];

       shadow_mat[2]  = -light_pos[2] * plane[0];
       shadow_mat[6]  = -light_pos[2] * plane[1];
       shadow_mat[10] = dot - light_pos[2] * plane[2];
       shadow_mat[14] = -light_pos[2] * plane[3];

       shadow_mat[3]  = -light_pos[3] * plane[0];
       shadow_mat[7]  = -light_pos[3] * plane[1];
       shadow_mat[11] = -light_pos[3] * plane[2];
       shadow_mat[15] = dot - light_pos[3] * plane[3];

       return shadow_mat;
}

Planlikning

Vi ser at for å kunne bruke skyggematrisen må vi først kjenne grunnplanets likning på formen ax + by + cz + d = 0. Denne kan vi finne med følgende metode:

//Finner planet på formen ax + by + cx + d,
//basert på tre kjente punkter i planet
//p1, p2, p3. a,b,c er normalen til planet,
public float [] calculatePlane(float p1[],float p2[],float p3[]){
    //Array for planlikningen
    float plane[] = new float[4];

    //Gitt to vektorer (tre punkter) i planet
    //kan normalen regnes ut
    plane[0] = ((p2[1]-p1[1])*(p3[2]-p1[2]))-
                             ((p2[2]-p1[2])*(p3[1]-p1[1]));
    plane[1] = ((p2[2]-p1[2])*(p3[0]-p1[0]))-
                             ((p2[0]-p1[0])*(p3[2]-p1[2]));
    plane[2] = ((p2[0]-p1[0])*(p3[1]-p1[1]))-
                             ((p2[1]-p1[1])*(p3[0]-p1[0]));
    plane[3] = -(plane[0]*p1[0] + plane[1]*p1[1] + plane[2]*p1[2]);


    return plane;
}

For å tegne skygge av et objekt på et gulv vil koden se omtrent slik ut i buffershadow. Koordinatene til gulv (floor[][]) er en global todimensjonal array. Vi har også deklarert arrayene plan_floor[] med fire elementer og shadow_floor[] med 16 elementer globalt.

public void init() {
         .......
         .......

    //Finner planet for gulv basert på tre kjente punkter
    float plane_floor[] = calculatePlane(floor[1],floor[2],floor[3]);
    //Lager shadowMatrix for gulv
    shadow_floor = shadowMatrix(plane_floor,light_position);

         .......
         .......
}

For enkelhets skyld har jeg kuttet ut å beskrive en del av de metodenen jeg bruker for å tegne skygge i buffershadow. Denne kan studeres nærmere ved å se på kildekoden. I dette eksempelet kan vi nå helt enkelt tegne gulv, objekt og skygge på gulv på denne måten.

public void display() {
            .......
            .......

       //Tegner gulv
       gl.glPushMatrix();
         drawFloor();
       gl.glPopMatrix();

       //Tegner skygge av objekt på gulv
       gl.glPushMatrix();
         gl.glMultMatrixf(shadow_floor);
         drawObject();
       gl.glPopMatrix();

       //Tegner objekt
       gl.glPushMatrix();
         drawObject();
       gl.glPopMatrix();

            .......
            .......
}

Dobbel blanding (Double Blending)

Det er imidlertid et par problemer forbundet med denne metoden, bortsett fra den helt åpenbare svakheten at objekter bare kan kaste skygge på kjente plan. Skyggen vil ligge i samme plan som grunnplanet. Dette fører til at skyggen "blandes" (stitching) med planet ettersom depth verdiene vil være tilnærmet like. Dette kan blant annet løses ved bruk av polygon offset. For å få en realistisk skygge ønsker vi å blande skyggen med material egenskapene til planet som skyggen kastes på. Dette er ikke helt enkelt. Problemet er at når skygge matrisen projiserer polygonene til et objekt på et plan, vil pixels kunne bli oppdatert mer enn en gang. Dette betyr at en bestemt pixel i skyggen blir blandet (blended) flere ganger, og skyggen blir for mørk i det aktuelle punktet. Dette problemet er kjent som dobbel blanding (dubbel blending). Viser et eksempel på hvordan dette kan se ut.

Stencil Buffer

Vi skal nå se litt på hvordan vi kan forbedre projeksjonsskygger ved hjelp av stencil buffer. Både dobbel blanding, avgrensing av skygge til planets utstrekning og "stitching" kan løses ved bruk av stencil buffer. Metoden går ut på å gi en unik ikke-null verdi til pixels som tilhører grunnplanet (eller planet som skal kastes skygge på). Igjen vil ikke kode eksemplene være helt likt som koden brukt i buffershadow. Jeg forenkler den litt her slik at den blir lettere å følge. Henviser igjen til kildekode for den spesielt interesserte.

  gl.glEnable(GL_STENCIL_TEST);
  gl.glStencilFunc(GL_ALWAYS, unique_stencil_value, ~0);
  gl.glStencilOp (GL_KEEP, GL_KEEP, GL_REPLACE);
  drawPlane();
  gl.glDisable(GL_STENCIL_TEST)

  //Vil bare oppdatere pixels som har unique_stencil_value
  //og tilbakestiller til null når pixels stencil verdi
  //er oppdatert
  gl.glDisable(GL_DEPTH_TEST);
  gl.glEnable(GL_STENCIL_TEST);
  gl.glStencilFunc(GL_EQUAL, unique_stencil_value, ~0);
  gl.glStencilOp(GL_KEEP,GL_KEEP,GL_ZERO);

  //Skrur på blending
  gl.glEnable(GL_BLEND);
  gl.glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
  //Skrur av lys for tegning av skygge uten normaler
  gl.glDisable(GL_LIGHTING);
  //Eksisterende farge (på plan) moduleres med 50% sort
  gl.glColor4f(0.0f,0.0f,0.0f,0.5f);

  //Tegner skygge av objekter på gulv
  drawObject();

  //Gjenoppretter original modus
  gl.glDisable(GL_BLEND);
  gl.glDisable(GL_STENCIL_TEST);
  gl.glEnable(GL_DEPTH_TEST);
  gl.glEnable(GL_LIGHTING);

Det vil kun være pixels som er assosiert med grunnplanets unike stencil verdi som blir oppdatert når skyggen rendres. Blending er skrudd på, men for å unngå dobbel blanding når et pixel blir oppdatert, må stencil verdi tilbakesettes til 0 slik at følgende pixel oppdateringer feiler stencil testen og blir eliminert.

En annen fordel ved bruk av stencil buffer er at bruk av polygon offset er overflødig. Depth testen er skrudd av under den stencil baserte renderingen av den projiserte skyggen.

buffershadow.java

Programmet buffershadow demonstrere bruk av stencil buffer for å kaste skygge på tre forskjellige plan, gulv og to vegger. Screenshot fra programmet buffershadow.java

Koden til buffershadow.java: buffershadow.java

Texturer brukt til programmet kan du se her:
kommode_front.png , kommode_texture.png , wood_light.png

Kommentar til buffershadow.java

Som tidligere nevnt er metoden med å bruke projeksjons matrisen for skyggelegging begrenset til å gjelde plan. Dette gjør at hvis vi ønsker at et objekt skal kaste skygge på et annet objekt, må vi finne likningen til hvert plan i objektet som skal skyggelegges. Da sier det seg selv at dette objektet ikke kan være veldig komplekst, og at det må bestå av definerte plan. Hvis vi skal være pirkete burde bordet i buffershadow ha kastet skygge på setet til den øverste stolen. Dette lar seg gjøre, selv om det ikke er implementert i buffershadow, ved å ta vare på modelview matrisen ved forskjellige stadier ved å bruke glGetFloatv(GL_MODELVIEW_MATRIX, modelview_matrix). Vi kunne funnet punktene til setet og regnet ut de forskjellige planene og skyggematrisene for så å rendre skygge på stolsetet. Men vi ser fort at det kan bli veldig mye regning i en scene med mange komplekse objekter. Derfor vil man etterhvert måtte vurdere å bruke helt andre metoder for skyggelegging av scener. Metoder for skygger på komplekse objekter blir beskrevet senere i modulen.

Ved å rotere hele scenen ser vi at skyggene til objektene blir tegnet på baksiden av gulv og vegger. I en scene som ikke skal kunne roteres er ikke dette av betydning ettersom skyggene på baksiden ikke vil vises. En annen, og kanskje litt grov måte å løse dette på, kan være å tegne doble vegger, slik at de nye planene dekker over skyggene.

Myk skygge (Soft Shadow)

Ved å legge til en funksjon for å rendre skyggen flere ganger og med en liten translasjon for hver rendering, kan vi oppnå en myk skygge (Soft Shadow). Metoden for å gjøre dette i buffershadow er kommentert ut ettersom det krever stor prosessorkraft å gjøre dette. Programmet tar derfor litt tid å starte på en gjennomsnitlig datamaskin. Den som ønsker kan gå inn i kildekoden og fjerne kommentartagene der det er anvist. Viser et screenshot fra buffershadow.java hvor "jitter" funksjonen er aktivisert.

Vi legger til hver rendering av skyggen i Accumulation buffer, og tegner så til slutt ut det endelige resultatet. Selveste metoden for å oppnå denne effekten kan implementeres i gl4java på denne måten

public void display() {
  .......
  .......

  float dx,dy,dz;
  dx = -0.2f;
  dy = 0.0f;
  dz = -0.2f;

  gl.glClear(GL_ACCUM_BUFFER_BIT);
  for (int i = 0; i<4; i++){
    dz+=0.1f;
    for (int j = 0; j<4; j++){
      dx+=0.1f;
      drawScene(dx,dy,dz);
      gl.glAccum(GL_ACCUM, 1.0f/16.0f);
    }
  }
  gl.glAccum(GL_RETURN, 1.0f);

  .......
  .......

Metoden drawScene utfører da selve rendringen og tar parameterene dx, dy og dz.

public void drawScene(float dx, float dy, float dz) {
  //Må tømme buffere for hver rendering
  gl.glClear(GL_COLOR_BUFFER_BIT |
             GL_DEPTH_BUFFER_BIT |
             GL_STENCIL_BUFFER_BIT);

  //Tegner plan
  gl.glPushMatrix();
    drawPlane();
  gl.glPopMatrix();

  //Tegner skygge. Blir translert med gitte parametre for
  //hver rendering av jitter-koden
  gl.glPushMatrix();
    gl.glMultMatrixf(shadow_floor);
    gl.glTranslatef(dx,dy,dz);
    drawObject();
  gl.glPopMatrix();

  //Tegner objekt
  gl.glPushMatrix();
    drawObject();
  gl.glPopMatrix();

Utvidelse av algoritme for projeksjons-skygger

Variasjoner og utvidelser av fremgangsmåten jeg har beskrevet i dette avsnittet kan implementeres. Det er ofte ønskelig å ha flere objekter som kaster skygge på flere plan. Det kan også være flere lyskilder i scenen som igjen skaper flere skygger fra hvert objekt.

Jeg vil henvise til pdf dokumentet "Improving Shadows and Reflections via the Stencil Buffer" av Mark J. Kilgard fra NVIDIA Corporation. Her finner man svært gode forklaringer og forslag til implementasjon av forskjellige skygge metoder. Dokumentet inneholder også en del eksempler på realisering av de forskjellige metodene og algoritmene i OpenGL kode.

Vi finner dokumentet på sidene til nvida
Dokumentet på pdf format kan lastes ned eller åpnes ved å følge denne linken: stencil.pdf

Skyggevolum

Ved bruk av skyggevolum, Shadow Volumes, vil hvert objekt som kaster skygge danne et område i rommet som vi definerer som Shadow Volume. Stencil buffer brukes så for å finne skjæringen mellom objekter i scenen og skyggen. Se figuren under.

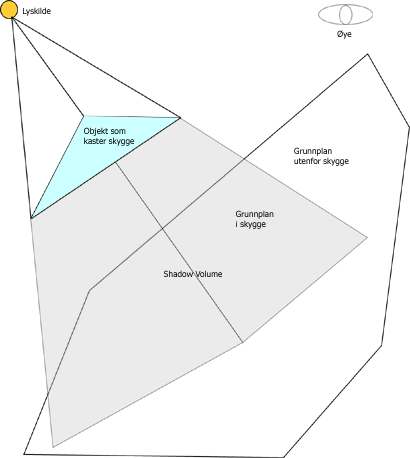
Shadow Volume blir konstruert ved at stråler fra lyskilden (Ray Tracing) skjærer hjørnene i objektet som skal kaste skygge, for så å fortsette ut av scenen. Dette gir oss en polygonal flate som inneholder objekter som ligger i skygge eller delvis i skygge. Stencil buffer blir brukt for å beregne hvilke deler av objektene i scenen som ligger innenfor skyggevolumet. For hvert pixel i scene vil stencil verdien økes hvis grensen til skyggevolumet "krysses" på vei inn i skyggen, og minske hvis grensen "krysses" på vei ut. Stencil operasjonen blir satt slik at den bare øker og minker når depth test passeres. Resultatet av dette er at alle pixels i scenen med stencil verdier som ikke er null vil identifisere de delene av et objekt som ligger innenfor skyggen.

Ettersom formen til skyggevolumet er bestemt av hjørnepunktene til objektet som kaster skygge, er det mulig å konstruere komplekse skyggevolumer.

Algoritmen for et enkelt objekt som kaster skygge og en lyskilde kan beskrives som følger:

1.  Color buffer og depth buffer blir åpnet for skriving og depth
    testing aktivisert
2.  Setter attributter for å tegne i skygge. Skrur av lyskilden
3.  Rendrer hele scenen
4.  Finner polygonenen som befinner seg innenfor skyggvolumet
5.  Slår av color og depth buffer for skriving,
    men lar fortsatt depth test være aktiv
6.  Setter stencil buffer til 0 hvis øyet befinner seg
    utenfor skyggevolum, 1 hvis innenfor.
7.  Setter stencil funksjon til alltid å passere.
8.  Setter stencil opperasjon til å øke hvis
    depth test passerer.
9.  Skru på back face culling
10. Rendrer skyggevolum polygonene
11. Setter stencil test til å minke hvis depth test passerer.
12. Skrur på front face culling
13. Rendrer skyggevolum polygonene
14. Setter stencil funksjon til å teste på om
    verdi er 0 (equal)
15. Setter stencil opperasjon til å gjøre ingenting
16. Skrur på lys
17. Rendrer hele scenen

Når hele scenen blir rendret andre gangen, vil kun pixels som har en stencil verdi lik 0 bli oppdatert. Siden stencil verdienen kun ble forandret når depth test passerte, vil denne verdien representere hvor mange ganger pixelets projeksjon passerte innenfor skyggevolumet minus det antallet det passerte utenfor skyggevolumet før det nærmeste objektet i scenen ble "truffet". Hvis grensen har blitt krysset et jevnt antall ganger vil pixelets projeksjon ha "truffet" et objekt som lå på utsiden av skyggevolumet. Pixlene på utsiden av volumet kan derfor "se" lyset, og det er derfor lyset blir skrudd på før den siste rendringen av scenen.

Når vi har kompliserte objekter som skal kaste skygge i en scene er det fornuftig å finne punktene som beskriver silhouetten til objektet og kun bruke disse i beregningen av skyggevolumet. Når objektene blir svært kompliserte ser vi at dette kan være en omfattende oppgave.

Fordeler og ulemper med skyggevolum

Algoritmen kan lett utvides til å omfatte flere lyskilder i en scene. For hver lyskilde repeterer vi den andre "runden" av algoritmen, setter stencil buffer til 0, beregner skyggevolum og rendrer for å oppdatere stencil buffer. Istedenfor å erstatte pixel verdien til objekter som ligger utenfor skygge, velger vi en passende blending funksjon og skrur på det aktuelle lyset.

Problemene med denne metoden oppstår når objektet som skal kaste skygge blir svært komplekst ettersom det da blir vanskelig å beregne riktig skyggevolum. Metoden krever også en inngående kjennskap til bruk av stencil og depth buffer.

Skyggekart

Skyggekart-teknikken, Shadow Maps, for skyggelegging av en scene bruker depth buffer og texture projeksjon. Scenen blir transformert slik at øyet ligger i punktet til lyset. Objektene i scenen blir rendret og depth buffer oppdatert. Vi har da fått "lysets depth buffer", dette kaller vi et shadow map. Shadow map brukes så til å dele inn scenen i to regioner, det som ligger innenfor skygge og det som ligger utenfor. Lysets depth buffer (Shadow map) brukes til å legge textur på den regionen som ligger i skygge.

Algoritmen for shadow maps kan beskrives som følger:

Algoritmen krever to rendringer
1. Gangs rendring
  1. Rendrer depth buffer fra lysets posisjon i rommet
     (Resultat er shadow map som brukes ved 2.gangs rendring)

2. Gangs rendring
  1. Rendrer scenen fra øyets posisjon i rommet. For hvert fragment
     som blir konvertert til vinduskoordinat (Rasterized):
      - Avgjør fragmentets XYZ posisjon i forhold til lyset
      - Sammenlign depth verdi for lysets posisjon XY i depth map
        med fragmentets lysposisjon Z

  2. A = Z verdi fra depth map ved fragmentets XY lysposisjon
     B = Z verdi for fragmentets XYZ lysposisjon

  3. Hvis B er større enn A må det være "noe" nærmere lyset enn
     det aktuelle fragmentet
      - Fragmentet blir skyggelagt

  4. Hvis A og B er omtrent like vil fragmentet ligge i lys

Fordeler og ulemper med skyggekart

Shadow maps har en stor fordel ettersom metoden ikke er avhengig av at vi finner silhouetten til objektene som skal kaste skygge. Vi trenger heller ikke klippe resultatet av skyggen. Et hvert objekt som kan rendres kan også kaste skygge ved hjelp av Shadow Maps.

Problemet er at ettersom en shadow map er bygd opp av punkter vil vi kunne få et aliasing problem. Når texturen blir lagt på er det ikke sikkert at formen til den originale skygge texel passer korrekt med pixel. Dette kan resultere i at grensene til skyggene vil se "hakkete" og ujevne ut. Vi kan også oppleve at objekter kaster skygge på seg selv.

Et spesialtilfelle oppstår hvis vi tenker oss en lyskilde omgitt av objekter som alle skal kaste skygge. Det blir svært vanskelig å implementere shadow map teknikken i denne scenen ettersom vi skaper shadow map ved å rendre hele scenen sett fra lysets posisjon i rommet. Men i dette tilfellet vil det være vanskelig å finne en passenede måte å gjøre nettop dette. Vi er avhengige av å rendre scenen 360 grader omkring lyset, noe som ikke er trivielt.

Dokumenter og whitepapers:
Søk på ACM Portal [5]

• Opacity Shadow Maps,
  Tae-Yong Kim, Ulrich Neumann
• Adaptive Shadow Maps,
  Randima Fernando, Sebastian Fernandez, Kavita Bala, Donald P. Greenberg
• Shadow Mapping with Todays OpenGL Hardware,
  Mark J. Kilgard
• Shadow Techniques Shadow Techniques,
  Sim Dietrich
• The Accumulation Buffer: Hardware Support for High-Quality Rendering,
  Paul Haeberli and Kurt Akeley
• Real-Time Shadows,
  Eric Haines, Tomas Moller
• Shadow Volume Reconstruction from Depth Maps,
  Michael D. McCool
• Projective Texture Mapping,
  Cass Everitt
• Rendering Antialiased Shadows with Depth Maps,
  William T. Reeves, David H. Salesin, Robert L. Cook
• Practical and Robust Stenciled Shadow Volumes for Hardware-Accelerated Rendering,
  Cass Everitt and Mark J. Kilgard
• Fast Shadows and Lighting Effects Using Texture Mapping,
  Mark Segal, Carl Korobkin, Rolf van Widenfelt, Jim Foran, Paul Haeberli
• Shadow Volume Reconstruction from Depth Maps,
  Michael D. McCool
• Hardware Shadow Mapping,
  Cass Everitt, Ashu Rege, Cem Cebenoyan
• Hardware Shadow Mapping,
  Cass Everitt, Ashu Rege, Cem Cebenoyan
• Shadow Mapping with Todays OpenGL Hardware,
  Mark J. Kilgard
• Improving Shadows and Reflections via the Stencil Buffer,
  Mark J. Kilgard
• Robust Stencil Shadow Volumes,
  Mark J. Kilgard
• Efficient Generation of Soft Shadow Textures,
  Michael Herf
• Second-Depth Shadow Mapping,
  Yulan Wang, Steven Molnar
• CASTING CURVED SHADOWS ON CURVED SURFACES,
  Lance Williams

Eksempel kode (gl4Java):

• simpleshadow.java
• buffershadow.java
• Kildekode, klasser og teksturer: alt.zip

Prosjektet skrevet om til JOGL/NetBeans , B. Stenseth mai 2010:

• simpleshadow: https://svnit.hiof.no/svn/psource/JOGL/shadow1
• buffershadow: https://svnit.hiof.no/svn/psource/JOGL/shadow2