Frames

Problemstilling

Anta at vi har en eller annen parametrisk kurve C(t). Vi ønsker å tegne en liten figur med jevne t-steg på denne kurven. Vi kan realisere dette ganske enkelt etter følgende kodeplan:

 while( t < t_max)
 {
   glPushMatrix();
   glTranslate(Cx(t),Cy(t),Cz(t));
   < tegn figur >
   glPopMatrix();
   t+=t_step;
 }
 

Dette går greit så lenge vi ikke stiller krav til figurens orientering i forhold til kurven, eller så lenge figuren ikke har noen orientering. F.eks. vil et perlekjede av kuler kunne tegnes greitt på denne måten.

Dersom figuren har en orientering må vi modifisere algoritmen:

 while( t < t_max)
 {
   tglPushMatrix();
   glTranslate(Cx(t),Cy(t),Cz(t));
   < roter figuren på plass >
   < tegn figur >
   glPopMatrix();
   t+=t_step;
 }

Problemet her er at linja roter figuren på plass kan være ganske slitsom å erstatte med kode. Det er dette problemet vi skal finne en generell løsningsmetode for.

Det vi er ute etter er en transformasjon som transformerer oss til et koordinatsystem på kurven, på det stedet vi ønsker og med de akseretninger vi ønsker.

Metoden

Metoden er slik at vi bestemmer retninger for de aksene vi ønsker i det nye koordinatsystemet, for så legge disse retningene, sammen med angivelse av det nye origo, inn i en samlematrise. Nedenfor er metoden beskrevet stegvis:

1. Vi begynner med å finne en vektor T som beskriver en av aksene i det koordinatsystemet vi ønsker. I de fleste tilfellene er det rimelig at en av aksene ligger "langs" kurven. Det vil si at vi ønsker å bruke kurvens deriverte som en akse: T(t)=C'(t). Vi skriver kun T i fortsettelsen, og vi forutsetter at alle vektorene vi ser på nedenfor er beregnet for en bestemt t-verdi.

2. Så ønsker vi å bestemme en vektor, B som er normal til den vi bestemte under pkt1. Vi ser at her har vi en stor grad av frihet. Vi må treffe en beslutning om hvilken retning vi vil velge. Vi kan i prinsipp velge en hvilken som helst vektor V, og finne B som kryssproduktet av T og V: B=T X V. Det eneste formelle kravet vi stiller til V er at den ikke faller sammen med (er colineær med) T. Hvis denne betingelsen er oppfylt vet vi at kryssproduktet ovenfor gir oss en vektor som er normal på T (og V). Valget av V er helt avgjørende for orienteringen av de to andre aksene i koordinatsystemet. Hills bok foreslår den dobbeltderiverte av kurven C''(t) som en kandidat for V. Vi skal se litt på dette nedenfor i eksemplene.

3. Så ønsker vi å bestemme en tredje vektor, N, som er normal til både T og B. Her har vi liten frihet. Valget vi traff under punkt 2 bestemmer også retningen på den tredje vektoren N. Vi beregner N som kryssproduktet av T og B. N = T X B

4. Vi ønsker å bearbeide de tre vektorene ,T B N, slik at de får lengde 1. Det vil si at de normaliseres. Vi skal altså arbeide videre med enhetsvektorene i det nye koordinatsystemet. Selve normaliseringen er grei. For en vektor A finner vi den normaliserte ved AN=A/|A|, der |A| er (a0*a0+a1*a1+a2*a2+a3*a3)^1/2. Vi fortsetter med betegnelsene T, B og N, og forutsetter at de er normaliserte.

5. Når de tre enhetsvektorene ,T B N, er bestemt kan vi formulere en matrise, M, som realiserer den ønskede transformasjonen. M får formen M=|T B N C|, eller utskrevet:

           |t0 b0 n0 c0|
           |t1 b1 n1 c1|
      M =  |t2 b2 n2 c2|
           |t3 b3 n3 c3|
       

   der C angir posisjonen på selve kurven. Alle vektorene, og derved matrisen er beregnet for en bestemt t-verdi.

Hvis vi ser litt på den matrisen vi har satt opp, så ser vi at kolonnen C på vanlig måte beskriver en translasjon. De tre første kolonnene er litt verre å skaffe seg et intuitivt inntrykk av. Vi går ikke inn på noen bevis for denne matrisen i dette materialet. Vi kan imidlertid konstatere at slik vi har formulert matrisen ovenfor så er T x-akse i det nye koordinatsystemet, B er y-akse og N er z-akse. Vi skal se litt nærmere på dette i eksemplene nedenfor.

Hvis vi går tilbake til problemstillingen vi reiste innledningsvis, kan vi reformulere tegnestrategien slik:

 while( t < t_max)
 {
   glPushMatrix();
   < beregn C,T,B,N og derved M for t>
   glMultMatrix(M);
   < tegn figur >
   glPopMatrix();
   t+=t_step;
 }
 

Spiral som eksempel

Vi vet fra modulen Parametrisk form at vi kan beskrive en spiral ved hjelp av en parameter t:

 C(t)= r·cos(2·pi·t), r·sin(2·pi·t), b·t
 

Vi går en runde i spiralen når t går fra 0 til 1 eller generelt fra i til i+1. På en runde stiger spiralen b. Vi antar for enkelhets skyld at radien, r, =1. Vi taper ikke noe i generalitet om vi skriver:

 C(t)=cos(t), sin(t), b·t
 

Det betyr bare at t må øke med 2·pi for at vi skal gå en runde og at stigningen blir b/2·pi.

Vi skal bruke metoden ovenfor, med Hills angivelser og vil da trenge både den deriverte og den dobbeltderiverte, og vi regner dem ut med det samme:

 C'(t)= -sin(t),  cos(t), b
 C''(t)=-cos(t), -sin(t), 0

Metodisk

Vi følger metoden som er beskrevet ovenfor:

1. Finn tangenten, T. Det er den deriverte og vi har

        T: (-sin(t),  cos(t), b)
        

2. Finn den andre aksen B som kryssproduktet av T og en "annen" vektor V. Vi velger den dobbeltderiverte som V og finner:

         B= T X C''
            (-sin(t), cos(t), b) X (-cos(t), -sin(t), 0)
            (-b·sin(t) , -b·cos(t) , 1)
         

3. Finn den tredje aksen N som kryssproduktet av T og B.

         N= T X B
            (-sin(t), cos(t), b) X (-b·sin(t) , -b·cos(t) , 1)
            ((1+b2)·cos(t),(1+b2)·sin(t),0)
         

4. Vi normaliserer de tre vektorene, T, B og N og får:

   

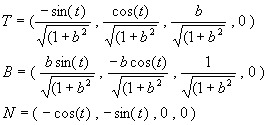
   Der vi har lagt til 0 som siste element i vektorene for å få den formen vi trenger i en 4 X 4 matrise.

5. Vi har funnet de tre akseretningene og har det vi trenger for å lage matrisen M=|B N T C|.

Algoritmen

Følgende algoritme tegner ut en spiral med en kjegle som har spissen mot økende t på spiralen, i "GL4Java inspirert pseudokode":

   // draw the helix with 10 windings
   double b=0.5;
   double ht=0.0;
   glBegin(GL_LINE_STRIP);
   while(ht<10.0)
   {
      glVertex3d(cos(ht*2*PI),sin(ht*2*PI),b*ht);
      ht+=0.02;
   }
   glEnd();

   // set up the 4 vectors we need for the FrenetFrame at t
   double n=sqrt(1+b*b);
   // the normalized derivative, tangent
   double T[]={-sin(t)/n,cos(t)/n,b/n,0.0};
   // the normalized crossproduct T x the double derivative
   double B[]={b*sin(t)/n,-b*cos(t)/n,1/n,0.0};
   // TxB, normalized
   double N[]={-cos(t),-sin(t),0.0,0.0};
   // and the origo
   double C[]={cos(t),sin(t),b*t,1.0};


   // set the matrix, NOTE: transposed compared to theory above
   double M[]={
               N[0],N[1],N[2],N[3],
               T[0],T[1],T[2],T[3],
               B[0],B[1],B[2],B[3],
               C[0],C[1],C[2],C[3],
              };

   // draw the  sylinder at position C[t]
   glPushMatrix();
   glMultMatrixd(M);
   qdh=gluNewQuadric();
   gluCylinder(qdh,0.0f,0.2f,0.3f,15,15);
   gluDeleteQuadric(qdh);
   glPopMatrix();

Et Java-program som implementerer tilsvarende: helix.java

Bezierkurve som eksempel

Vi kikker litt nærmere på en mer generell kurveform: Bezierkurven. Vi nøyer oss med å se på en kubisk kurve. Vi vet fra modulen Bezier at Bezierkurven, den deriverte og den dobbeltderiverte kan vi framstille slik ( vi bruker C for å angi kurven for å bruke samme betegnelse som over):

 C(t)=  P0(-t3+3t2-3t+1) + P1(3t3-6t2+3t) + P2(-3t3+3t2) + P3(t3)

 C'(t)= P0(-3t2+6t-3) + P1(9t2-12t+3) + P2(-9t2+6t) + P3(3t2)

 C''(t)=P0(-6t+6) + P1(18t-12) + P2(-18t+6) + P3(6t)
 

Metodisk

Vi regner oss ikke analytisk fram til alle vektorene vi trenger. Det er like greitt å gjøre dette numerisk, i selve programmet. Vi bruker samme framgangsmåten som vi brukte for spiral:

   T=C'
   B=T x C''
   N=T x B
   

Hvis vi gjennomfører resonnementet som ovenfor vil vi få et problem med akseorienteringen. Dersom vi tegner ut aksene slik vi finner dem, vil vi få et resultat som til høyre. Dette skyldes bruken av den dobbelderiverte som grunnlag for beregning av B. Den dobbelderiverte endrer retning underveis. Konsekvensen av dette er ikke merkbar dersom den figuren vi tegner er lik i zx- og zy-projeksjonen.

En korreksjon av dette kan vi søke ved å finne en annen vektor en den dobbelderiverte i bestemmelsen av B. Vi kan f.eks.forsøke oss med V=(0.0 , 0.0 , 1.0 , 0.0).

   T=C'
   B=T x V
   N=T x B
   

Hvorvidt dette er de retningene vi ønsker er en sak for seg, men vi har ialle fall greidd å unngå den plutselige, ukontrollerte endringen i aksenes retning. En nærmere analyse av anatomien i disse Frenet matrisene kan hjelpe oss å finne ønskede løsninger. Blandt annet kan vi i stedet for M=|B N T C| skrive M=|T B N C| og på den måten legge x-aksen langs tangenten.

Algoritmisk

Programmet tube, se referanser, legger korte sylindere langs en Bezierkurve. Et pent rør er avhengig av sylinderenes lengde og avstanden mellom dem.

Siden vi har valgt å beregne vektorene numerisk trenger vi et hendig apparat for å regne kryssprodukter av vekktorer og for å normalisere vektorer. Hvis vi dessuten skal tegne bezierfunksjonen for hånd, trenger vi noen hjelperutiner for å regne ut Bezierverdier. Algoritmen nedenfor er en grov skisse basert på CStdView::DrawScene i programmet tube, stdview.cpp, og forutsetter en del hjelpefunksjoner.

// Bezier, Derivative of Bezier and
// double derivative are all prepared in
// bez, d_bez and dd_bez

// the Bezier function
CMaterial::SetMaterial(RED_PLASTIC);
glLineWidth(4);
drawBezier();

// do the t-walk and draw in frenet frames
int ix=0;
while(ix<;PCNT)
{

   // Bezier is now tabulated in:
   // (bez[ix][0],bez[ix][1],bez[ix][2])
   // The derivative (tangent) is tabulated in:
   // (d_bez[ix][0],d_bez[ix][1],d_bez[ix][2])
   // The double derivated is tabulated in:
   // (dd_bez[ix][0],dd_bez[ix][1],dd_bez[ix][2])

   // finding the normalized tangent:
   // T pointing along the curve
   v3d T(d_bez[ix][0],d_bez[ix][1],d_bez[ix][2]);
   T.normalize();

   // finding the normalized d cross dd vector:
   // B pointing perpendicular to T
   v3d B(d_bez[ix][0],d_bez[ix][1],d_bez[ix][2]);
   B.cross(dd_bez[ix][0],dd_bez[ix][1],dd_bez[ix][2]);
   B.normalize();

   // if we are not happy with the doublederivative
   // as basis for the second vector
   // maybe we can use an other vector here ?
   // what is the effect of a fixed direction ?
   // B.cross(0.0f,0.0f,1.0f);
   // B.normalize();

   // finding a third perpendiculat vector:
   // N perpendicular to both T and B
   v3d N(B.x,B.y,B.z);
   N.cross(T);  // and it is normalized since B and T are

   // we want to move to the correct point on the Beziercurve
   // as tabulated in (bez[ix][0],bez[ix][1],bez[ix][2])
   v3d C(bez[ix][0],bez[ix][1],bez[ix][2]);

   // at this point T,B,N describes the coordinate system
   // we will use at the position C
   // N will act as x-axes
   // B will act as y-axes
   // T will act as z-axes

   // setting up the matix that will take us to the
   // Frenet frame located at this t-point
   // M=|N,B,T,C|, where C is the Bezier itself
   // note transpose of matrix

   GLfloat M[16]={
      N.x,N.y,N.z,0,
      B.x,B.y,B.z,0,
      T.x,T.y,T.z,0,
      C.x,C.y,C.z,1
   };

   glPushMatrix();
   glMultMatrixf(& M[0]);
   // and we are ready to draw what ever we want to draw
   // the green tubes
   // draw a sylinder as a temporary solution
   GLUquadricObj *glpQ=gluNewQuadric();
   CMaterial::SetMaterial(EMERALD);
   gluCylinder(glpQ,1.1f,1.1f,1.0f,15,1);
   gluDeleteQuadric(glpQ);
   glPopMatrix();

   ix++;
}
 

Generalisert

I begge eksemplene ovenfor har vi sett på funksjoner som er analytisk beskrevet og er deriverbare. Vi har dratt nytte av dette når vi har beregnet en av aksene som tangenten til kurven. Spiralen er et spesielt eksempel. Bezierkurven gir oss stor grad av fleksibilitet og er generelt nyttig. Vi kan tenke oss andre funksjoner med tilsvarende behagelige egenskaper. Spesielt nærliggende er kurver beskrevet ved trigonometriske funksjoner.

Vi kan jo imidlertid tenke oss at vi har et tilsvarende problem i en situasjon der kurven er beskrevet ved en serie punkter. Vi har altså ingen analytisk måte å finne den deriverte på. Vi vil kunne anvende et helt tilsvarende resonnement i slike tilfeller. Problemet med å finne tangenten blir litt annerledes. Hvis det er en sammenheng i punklista i den forstand at de beskriver en eller annen slags bane, kan vi kanskje bruke vektoren fra et punkt til det neste som tangent. Hvis det ikke er slik har vi en annen og helt åpen situasjon og kriteriene for å velge akseretninger vil være andre og situasjonsbestemte.

Et interesant spesialtilfelle der vi kan vurdere Frenet Frames er når vi ønsker at figur B i posisjon PB skal være orientert mot figur A i posisjon PA når figur A beveger seg. Vektoren PB->PA vi i dette tilfellet kunne tjene som kandidat for en av aksene i Frenet koordinatsystemet, altså det koordinatsystenmet vi vil tegne B i.

• tube tube.zip(VC++/gml), tube.zip(VC++/.Net)

• helix: https://svnit.hiof.no/svn/psource/JOGL/helix
• tube: https://svnit.hiof.no/svn/psource/JOGL/tube