Textur
Normaler
Grafikk
Børre Stenseth
Å tegne:>Fotball

Fotball

Geometri

buckyflat

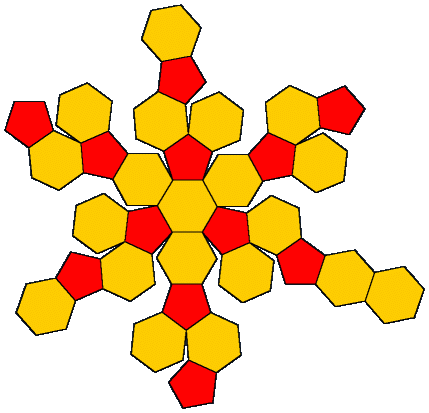
"Buckyball" er et kjent fenomen både i matematikken, naturen og på fotballbanen. Formen på en buckyball er beskrevet ved hjelp av det gyldne snitt (1.61803399...). Dette forholdstallet kan beregnes som kvotienten mellom to nabotall i Fibonacci-rekka og det inngår i mange resonnementer i matematikken og det finnes i naturlige former. Det tillegges også en estetisk betydning som et "naturlig" eller balansert forhold, f.eks. som forholdet mellom høyde og bredde i et rektangel. Det ser ut til at det gyldne snitt i en del sammenhenger beskriver fenomener som er forbundet med maksimal pakking av former.

Buckyball er et kjent begrep for kjemikere og beskriver en ordning av 60 carbonatomer i hjørnene til figuren. Figuren er oppkalt etter R. Buckminster Fuller.

En buckball har 60 hjørner, 20 6-kanter og 12 5-kanter. Figuren er fra GoldenNumber.net [1] .

Dataene som er brukt til å tegne buckyball i denne modulen ser du her, i C#-syntax:datadef.html

Når vi skal tegne en slik figur med flater, lys og egenskygge, er det viktig at vi ordner punktene i et polygon konsekvent. Det vil si at vi må beskrive alle polygoner enten med eller mot klokka. For at dette skal ha mening må vi definere et ståsted. En fruktbar modell er å si at vi står foran fronten på polygonet og nevner hjørnene mot klokka (OpenGL default). Vi kan omdefinere hva som er foran og bak ved følgende OpenGL-kommandoer: 

glFrontFace(GL_CW)
glFrontFace(GL_CCW)

Der vi kan sette retningen med klokka (CW) eller mot klokka (CCW), sett mot fronten.

Når vi har fått orden på dette, kan vi regne ut alle normalene vi trenger ved å ta kryssproduktet av to vektorer i flaten. For våre data kan det gjøres slik, bare vist for polygonene med 6 kanter. 

static void PrepareData()
  {
      // calculate normals for pol6:normal6 and pol5:normal5
      // Cross product is used:c=axb=(a2b3-a3b2, a3b1-a1b3, a1b2-a2b1)
      // The normals are normalized (length=1)
      for (int ix = 0; ix < 20; ix++)
      {
          float ax = pol6[ix, 2, 0] - pol6[ix, 0, 0];
          float ay = pol6[ix, 2, 1] - pol6[ix, 0, 1];
          float az = pol6[ix, 2, 2] - pol6[ix, 0, 2];
          float bx = pol6[ix, 3, 0] - pol6[ix, 0, 0];
          float by = pol6[ix, 3, 1] - pol6[ix, 0, 1];
          float bz = pol6[ix, 3, 2] - pol6[ix, 0, 2];
          float x = ay * bz - az * by;
          float y = az * bx - ax * bz;
          float z = ax * by - ay * bx;
          float l=(float)Math.Sqrt(x*x+y*y+z*z);
          normal6[ix,0]=x/l;
          normal6[ix,1]=y/l;
          normal6[ix,2]=z/l;
      }
      ...
  }

Selve uttegningen av polygoner er rett fram: 

static void DrawBuckyBall()
{
    int mode = Gl.GL_POLYGON;
    // polygons with 6 edges
    SetWhiteMaterial();
    for (int p = 0; p < 20; p++)
    {
        Gl.glBegin(mode);
        Gl.glNormal3f(normal6[p, 0], normal6[p, 1], normal6[p, 2]);
        for (int ix = 0; ix < 6; ix++)
            Gl.glVertex3f(pol6[p, ix, 0], pol6[p, ix, 1], pol6[p, ix, 2]);
        Gl.glEnd();
    }
    // polygons with 5 edges
    SetBlackMaterial();
    for (int p = 0; p < 12; p++)
    {
        Gl.glBegin(mode);
        Gl.glNormal3f(normal5[p, 0], normal5[p, 1], normal5[p, 2]);
        for (int ix = 0; ix < 5; ix++)
            Gl.glVertex3f(pol5[p, ix, 0], pol5[p, ix, 1], pol5[p, ix, 2]);
        Gl.glEnd();
    }
 }

Textur

Vi ønsker å legge en tekstur på alle 6-kantene. Vi tar utgangspunkt i en kvadratisk tekstur og vil finne hvilke koordinater i teksturen vi vil mappe til 6-kantenes hjørner.

one6p

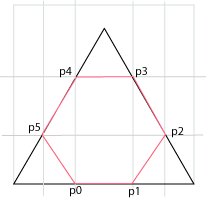
Ut fra figuren ser vi at:

p0d/3 , 0
p12d/3 , 0
p2d-(d/3)cos(60) , (d/3)sin(60)
p3d-(2d/3)cos(60) , (2d/3)sin(60)
p4(2d/3)cos(60) , (2d/3)sin(60)
p5(d/3)cos(60) , (d/3)sin(60)

der d er siden i trekanten og kvadratet. Når vi oppgir koordinater i en bitmap, som i algoritmen nedenfor, har d alltid verdien 1, uavhengig av dimensjonene på bitmapen i pixler. En bitmap har logisk utstrekning fra (0,0) til (1,1).

ronald

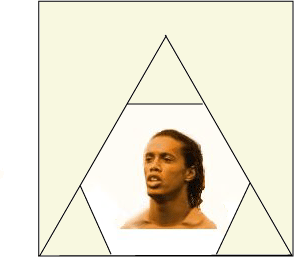
Siden OpenGL bare vil ha teksturer som har formatet: 2n*2m, må vi forsyne programmet med bitmapper der vi har plassert den figuren vi vil vise slik at den faller innenfor den trekanten vi har antydet på figuren ovenfor. Dersom vi (av mangel på fantasi) vil tegne dette bildet som er 256 x 256 pixler på hver av 6-kantene, så må vi plassere det vi vil vise fram i følge resonnementet over. Dersom vi ikke vil ha en forvrengning av bildet.
ronalball

Teksturmappingen for 6-kantene settes opp slik i arrayen tex6: 

// calculate mapping coordinates for texture
float d=1.0f;
float cos60=(float)Math.Cos(Math.PI/3.0);//60 degrees
float sin60=(float)Math.Sin(Math.PI/3.0);
tex6[0,0]=d/3.0f;                   tex6[0,1]=0.0f;
tex6[1,0]=2.0f*d/3.0f;              tex6[1,1]=0.0f;
tex6[2,0]=d-(d/3.0f)*cos60;         tex6[2,1]=(d/3.0f)*sin60;
tex6[3,0]=d-(2.0f*d/3.0f)*cos60;    tex6[3,1]=(2.0f*d/3.0f)*sin60;
tex6[4,0]=(2.0f*d/3.0f)*cos60;      tex6[4,1]=(2.0f*d/3.0f)*sin60;
tex6[5,0]=(d/3.0f)*cos60;           tex6[5,1]=(d/3.0f)*sin60;

Uttegningen blir slik: 

static void DrawBuckyBall()
{
    int mode = Gl.GL_POLYGON;
    // polygons with 6 edges
    SetWhiteMaterial();
    for (int p = 0; p < 20; p++)
    {
        Gl.glBegin(mode);
        Gl.glNormal3f(normal6[p, 0], normal6[p, 1], normal6[p, 2]);
        for (int ix = 0; ix < 6; ix++)
        {
            Gl.glTexCoord2f(tex6[ix, 0], tex6[ix, 1]);
            Gl.glVertex3f(pol6[p, ix, 0], pol6[p, ix, 1], pol6[p, ix, 2]);
        }
        Gl.glEnd();
    }
    // polygons with 5 edges, no texture
    SetBlackMaterial();
    for (int p = 0; p < 12; p++)
    {
        Gl.glBegin(mode);
        Gl.glNormal3f(normal5[p, 0], normal5[p, 1], normal5[p, 2]);
        for (int ix = 0; ix < 5; ix++)
            Gl.glVertex3f(pol5[p, ix, 0], pol5[p, ix, 1], pol5[p, ix, 2]);
        Gl.glEnd();
    }
 }

Innlastingen og prepareringen av bitmaps er f.eks. slik: 

// holding a texture, need a reference variable
private static int[] texture = new int[1];

static void LoadTexture()
{
    // get a bitmap
    //string filename = Application.StartupPath + "\\Marrakech.jpg";
    //string filename = Application.StartupPath + "\\chesspiece.gif";
    string filename = Application.StartupPath + "\\ronaldinho.jpg";
    //string filename = Application.StartupPath + "\\cloth.bmp";
    Bitmap bm = new Bitmap(filename);
    
    // set up texture
    if (bm != null)
    {
        // get a place to store texture
        Gl.glGenTextures(1, out texture[0]); 
        // rotate the nbitmap
        bm.RotateFlip(RotateFlipType.RotateNoneFlipY);
        
        // Lock bitmap in rectangle
        Rectangle rectangle = new Rectangle(0, 0, bm.Width, bm.Height);
        // Fill the rectangle with a given format
        BitmapData bitmapData = bm.LockBits(rectangle, 
            ImageLockMode.ReadOnly, 
            PixelFormat.Format24bppRgb);
        // Tekstur generering
        Gl.glBindTexture(Gl.GL_TEXTURE_2D, texture[0]);                
        Gl.glTexImage2D(Gl.GL_TEXTURE_2D, 0, Gl.GL_RGB8,
                        bm.Width, bm.Height, 0,
                        Gl.GL_RGB, Gl.GL_UNSIGNED_BYTE, bitmapData.Scan0);
        // try Gl.GL_RBG for Gl.GL_RGB above
        Gl.glTexParameteri(Gl.GL_TEXTURE_2D, 
                        Gl.GL_TEXTURE_MIN_FILTER, Gl.GL_LINEAR);
        Gl.glTexParameteri(Gl.GL_TEXTURE_2D, 
                        Gl.GL_TEXTURE_MAG_FILTER, Gl.GL_LINEAR);
        if (bm != null)
        {
            bm.UnlockBits(bitmapData); // Release
            bm.Dispose();              // Dispose 
        }
    }
    else
        MessageBox.Show("Ingen bitmap", "ERROR",
                        MessageBoxButtons.OK, MessageBoxIcon.Error);
}

Grid

grid

Vi ønsker å tegne ut en buckyball som en enkel grid med kuler i de 60 hjørnene i stedet for å legge tekstur på noen av flatene.

Vi merker oss at siden vi har 12 5-kanter som ikke er naboer, er det tilstrekkelig å tegne kuler i hjørnene på 5-kantene.

Uttegningen kan være som nedenfor. Alle linjer blir tegnet to ganger, men kulene bare en. 

static void DrawBuckyBall()
{
    Gl.glClearColor(1.0f, 1.0f, 1.0f, 1.0f);
    int mode = Gl.GL_LINE_LOOP;
    // polygons with 6 edges
    SetWhiteMaterial();
    for (int p = 0; p < 20; p++)
    {
        Gl.glBegin(mode);
        for (int ix = 0; ix < 6; ix++)
        {
            Gl.glVertex3f(pol6[p, ix, 0], pol6[p, ix, 1], pol6[p, ix, 2]);
        }
        Gl.glEnd();
    }
    // polygons with 5 edges
    for (int p = 0; p < 12; p++)
    {
        Gl.glBegin(mode);
        for (int ix = 0; ix < 5; ix++)
            Gl.glVertex3f(pol5[p, ix, 0], pol5[p, ix, 1], pol5[p, ix, 2]);
        Gl.glEnd();
    }
    // spheres in corners
    SetBlackMaterial();
    Glu.GLUquadric q;
    q = Glu.gluNewQuadric();
    for (int p = 0; p < 12; p++)
        for (int ix = 0; ix < 5; ix++)
        {
            Gl.glPushMatrix();
            Gl.glTranslatef(pol5[p, ix, 0], pol5[p, ix, 1], pol5[p, ix, 2]);
            Glu.gluSphere(q, 0.1, 20, 20);
            Gl.glPopMatrix();
        }
    Glu.gluDeleteQuadric(q);
}
[2] [3] [4] [5]

Kode

  • Buckyball med tekstur (Csharp/glut): https://svnit.hiof.no/svn/psource/CsharpGrafikk/taobuckyball
  • Buckyball( JOGL/Netbeans): https://svnit.hiof.no/svn/psource/JOGL/bucky
Referanser
  1. Bucky BallsGOLDENNUMBER.NETwww.goldennumber.net/buckyball.htm14-10-2011
  1. Computer Graphics Using OpenGL, 3nd editionF.S. Hill, S.M Kelly2001Prentice Hall0131496700
  1. Fibonacci Numbers and the Golden SectionRon Knottwww.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fib.html14-04-2010
  1. Buckyballs – a new sphere of scienceAustralian Academy of Sciencewww.science.org.au/nova/024/024key.htm14-04-2010
  1. R. Buckminster FullerNew Civilization Networkwww.newciv.org/whole/bucky.html14-04-2010
Vedlikehold

B Stenseth, januar 2006

Å tegne:>Fotball
til toppen
WXT 6
Valid HTML5
Valid CSS!