Modellering av fisk i 3D

Hva

Prosjektet mitt har vært å lage en fisk. Denne fisken har jeg prøvd å lage så realistisk som mulig. Fisken skulle kunne "svømme" og bevege seg langs en gitt kurve på skjermen. For å få bedre kontroll på prosjektet har jeg delt det inn i hovedtemaer. Disse er som følger:

Bezierflater og Bezierkurver
Tekstur
Animasjon
Frames
Fog eller tåke.

Modulen er delt inn i seksjoner som omhandler de foskjellige hoveddelene. Hovedvekten er lagt på animasjon og frames delene av modulen. De andre tre delene er bare forklart ganske overfladisk.

Bezierflater

Generelt

Før en ser på en bezier flate, kan det være hensiktsmessig å se på en enkel bezier kurve. En enkel bezier kurve har to endepunkt. Disse endepunktene gjenspeiler faktiske koordinater hvor kurven starter og slutter. I tillegg til disse punktene så har du 2 eller flere kontrollpunkter. Det er kontrollpunktene som bestemmer kurvens form. I figuren under ser vi på bildet til høyre at kontrollpunktene er plassert over og under, dette skaper en bølgeformet bezierkurve, mens på bildet til venstre er begge plassert på oversiden noe som ligner en halvsirkel.

Bezierflater blir definert ved å bruke to eller flere bezierkurver, for så å beregne verdier mellom kurvene. Bezierflater er anvendelige når man skal beskrive figurer som ikke så enkelt lar seg beskrives av fikanter, sirkler og andre geometriske primitiver. Formålet med bezierflater er altså å kunne beskrive avanserte geometriske former med relativt få parametre.

OpenGL og bezierflater

Tegning av bezierflater i Open GL er ganske enkelt. Det vanskeligste er å finne de riktige kontrollpunktene slik at flaten blir slik man vil ha den. Koden under tegner ut en bezierflate som har formen som en trekant. Dersom en ønsker krumming av noe slag, er det bare å endre på noen z-verdier.

float liste[] = {	// X     Y     Z
			0.0f, -4.0f, 0.0f,
			5.0f,  0.0f, 0.0f,
  			0.0f, -2.0f, 0.0f,
	  		5.0f,  0.0f, 0.0f
		  	,
	  		0.0f, 2.0f, 0.0f,
	  		5.0f, 0.0f, 0.0f,
  			0.0f, 4.0f, 0.0f,
	  		5.0f, 0.0f, 0.0f,
  			};

gl.glMap2f(GL_MAP2_VERTEX_3, 0.0f, 1.0f, 3, 2, 0.0f, 1.0f, 6, 4, liste);
gl.glEnable(GL_MAP2_VERTEX_3);
gl.glMapGrid2f(20, 0.0f, 1.0f, 20, 0.0f, 1.0f);
gl.glEvalMesh2(GL_LINE, 0, 20, 0, 20);

Kort forklaring er som følger:

glMap2f() definerer hvordan Bezierflaten skal tolkes av OpenGL. Viktigste er at den 5, 8 og 9 parametren er riktig.
glEnable() aktiviserer GL_MAP2_VERTEX3, viktig for å få opp noe i det hele tatt.
glMapGrid2f(), sier hvordan flaten skal tegnes, med tanke på antall ruter og detaljnivå.
glEvalMesh() tegner flaten, enkelte parameterverdier samsvarer med verdiene i glMapGrid2f(). Verdt å merke seg at man enten kan bruke GL_LINE eller GL_FILL. For å vise tekstur må en bruke den siste.

For mer inngående forklaring av koden så viser jeg til modulene Bezier-kurven, Bildebok, Farrisflaske, Monster og Påskeegg.

Bezierflatene til fisken min

Hele fisken min er utelukkende bygd opp av bezierflater. Fisken består av en flate for selve kroppen, en flate for halen, en for ryggfinnen, en for hver av sidefinnene og en for øyene.

Av alle disse flatene var det fiskekroppen som var den vanskeligste å lage, og også den jeg brukte lengst tid på.

I denne delen vil jeg ikke gå i detaljer på kode og koordinater, men heller vise en mer generell fremgangsmåte, og hvordan man kan tenke i form av kontrollpunkter for å få ønsket form.

Fiskekroppen

I utgangspunktet ville jeg utnytte strømlinjeformene til fisken til min egen fordel. Ettersom fisken er strømlinjeformet så tenkte jeg her først på å lage to halvdeler og sette sammen til en fisk, på den måten trengte jeg bare å lage bezierflate for den ene siden av fisken, for så å rotere flaten om x-aksen. Med dette som utgangspunkt så lagde jeg noen enkle skisser. Fisken var i utgangspunktet strømlinjeformet og bestod i grunnen av ellipser. Ut fra disse betraktningene så lagde jeg en enkel skisse av hvordan fisken kunne bli relaisert, jeg lagde også et enkelt fiskeskall basert på denne skissen:

fiskenTegnet3D forsteFisk

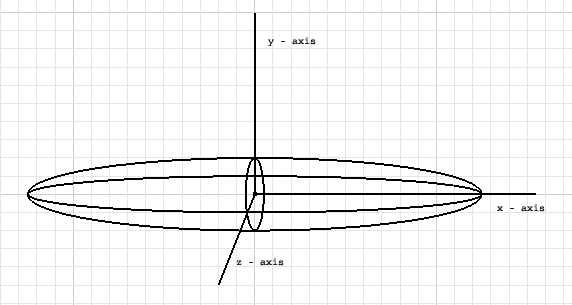
Denne første fisken var lagd med utgangspunkt i en to delings strategi, tanken var å tegne den ene siden av fisken, for så å rotere og tegne den andre siden. Dette var et godt utgangspunkt, men det viste seg også at en slik strategi hadde sine svakheter. For at strategien skulle fungere måtte fisken være konform alle veier. Hovedårsaken til at denne strategien ble lagt til side var problemer vedrørende animasjonen av fisken. Løsningen var å gå over til å bare bruke en bezierflate for å representere fiskekroppen. Denne bezierflaten fikk hele 9 kontrollkurver.

Figuren over viser kontrollpunktene til kurvene i xy planet, dvs 5 av de. De fire nederste kontrollkurvene gjentar seg selv på "baksiden" av xyplanet, men med andre z-koordinater, se figuren til høyre. Dette er altså de kontrollpunktene som jeg fikk til slutt, dette er fisken sett fra "siden" altså i XY planet. Under ser vi grid av hvordan den ferdige fiskekroppen ble. gridBody

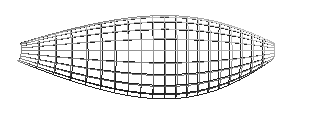
For å få koordinatene til selve fiskekroppen er det bare å se i filen Fish.java.

Halefinnen

Dette var helt klart den enkleste finnen. Jeg kunne valgt å lage en vanskelig halefinne, men kom frem til at det var mest hensiktsmessig med en enkel en. Halefinnen ser i utgangspunktet ut som en trekant. Det enkleste var å lage en bezierflate som en trekant og dreie denne om sin egen akse, for så å tegne den på nytt på baksiden.

gridTailFin

Ryggfinnen

Voldte meg en del mer problemer. Denne finnen skulle stikke opp på ryggen til fisken. Finnen skulle være tynn, men ikke helt tynn. Med tanke på at en fisk er et veldig strømlinjeformet dyr, så var det ønskelig at ryggfinnen hadde formen til en flyvinge.

backFin2 backFin3

Figurene ovenfor viser et par tidlige skisser over hvordan jeg ville at ryggfinnen skulle se ut. Figuren til venstre viser finnen sett ovenfra, mens det til høyre viser finnen sett fra siden.

Resultatet ble slik:

gridBackFin

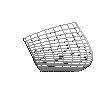
Finnen er ganske mye større en det som vises på fisken. Men det overflødige av finnen kunne jeg "gjemme" nede i fisken, på den måten ungikk jeg også unødige gliper mellom finnen og selve fiskekroppen.

Sidefinnene

Sidefinnene ville jeg også holde så enkle som mulig. Disse finnene er ment som styrefinner for de fleste fisker. Den enkleste formen er å lage dem som en rettvinklet trekant, men med en noe butt ende.

Øyene

Var heller ikke så lett å få til, men det var allerede gjort lignende så jeg hadde koordinater å ta utgangspunkt i. Disse koordinatene modifiserte jeg og tilpasset slik at de passet til mitt formål.

Det neste målet var å få sydd sammen alle delene slik at jeg til slutt hadde noe som liknet på en fisk. Hele aksesystemet mitt tok utgangspunkt mitt i fisken, så det var å regne seg utifra sentrum. For å tegne ut fisken så lagde jeg en makeFish() metode. Denne metoden hadde flere submetoder som tegnet ut de ulike delene av fisken. Ved å bruke push og pop, så kunne jeg ved hver gang jeg begynte på en ny subrutine, ta for gitt at jeg var tilbake i utgangspunktet til fisken, på den måten var det bare å regne seg ut til hvor de ulike delene skulle sitte.

gl.glPushMatrix();
drawFishBody();
gl.glPushMatrix();
drawTail();
gl.glPopMatrix();
gl.glPushMatrix();
drawBackFin();
gl.glPopMatrix();
gl.glPopMatrix();

Utdrag fra en drawBackFin():

gl.glRotatef(-90, 0.0f, 0.0f, 1.0f);
gl.glTranslatef( -0.6f *  myFish.getFactor(),0.5f * myFish.getFactor(), 0.0f);
gl.glMap2f(GL_MAP2_VERTEX_3, 0.0f, 1.0f, 3, myFish.getBackFin().getUN(), 0.0f, 1.0f,
				3*myFish.getBackFin().getUN(),
				myFish.getBackFin().getVN(), myFish.getBackFin().getBackFinCoord());
gl.glMapGrid2f(20, 0.0f, 1.0f, 20, 0.0f, 1.0f);
gl.glEvalMesh2(GL_FILL, 0, 20, 0, 20);

Fra koden over ser vi at finnen først roteres -90 grader om z aksen. Dette var for å få finnen til å stå riktig. Deretter skal finnen flyttes til riktig sted i koordinatsystemet. Dette gjøres ved å bruke glTranslatef(). Først flyttes finnen 0.6f i x retning og så 0.5 i y retning. Begge tallene multipliseres med en factor, denne factoren omtales mer i skalering. Etter at finnen er flyttet på plass er det bare å tegne den ut.

Resultatet ble som følger:

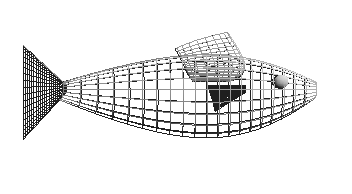
Fra figuren kan en helt klart se at ryggfinnen sitter et lite stykke ned i selve fisken.

Skalering

Som tidligere nevnt så multipliseres enkelte tall med en factor. Bakgrunnen for denne factoren er at det er en skaleringskonstant som gjør at en kan lage fisken i forskjellige størrelser. Denne størrelsen sendes inn som en parameter når man oppretter et fiske objekt. Verdier under 1.0 gjør fisken mindre, mens verdier over 1.0 gjør fisken større. Grunnen til at denne skaleringsfaktoren er med i gl.Translatef() er for at fisken skal bli tegnet ut riktig i forhold til den størrelsen som fisken har. Uten en slik skalering, kunne f.eks ryggfinnen forsvunnet ned i fisken.

Tekstur

Generelt

Tekstur kan være viktig og ønskelig for å gjøre et objekt mer virkelighetsnært. Tekstur er relativt enkelt å legge på objekter, det vanskeligste med teksturer er å lage dem slik at de blir bra. En bra tekstur kan utgjøre stor forskjell på det ferdige produktet. Det er mulig å legge tekstur på alle flater, men ettersom min modul dreier seg utelukkende om bezierflater så vil jeg fokusere mest på teksturere på bezierflater. Ettersom de ulike bezierflatene skal ha ulik tekstur skal jeg også vise hvordan man enkelt kan utvide en grunnleggende metode til å lese inn flere teksturer på en gang. Det viktigste å bite seg merke i før vi starter er at alle bilder som skal brukes som tekstur må være på binær form , av typen 2x. Bildet må dog være minst 64x64 pixler. Når bildet ditt er klart kan vi gå videre, det neste blir å lage en metode som kan laste inn bildet fra fil. Jeg vil presisere at begge de to neste metodene baserer seg på png-format. Det er selvsagt fullt mulig å bruke andre format.

Først en metode som laster et bilde. Metoden tar inn en parameter, filnavnet.

public void loadTexture(String filename) {
	PngTextureLoader texLoader = new PngTextureLoader(gl, glu);
	texLoader.readTexture(filename);
	if(texLoader.isOk()) {
		gl.glGenTextures(1, texture);
		gl.glBindTexture(GL_TEXTURE_2D, texture[0]);
		gl.glTexEnvf(GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE, GL_MODULATE);
		gl.glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_NEAREST);
		gl.glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
		gl.glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_REPEAT);
		gl.glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_REPEAT);
		gl.glTexImage2D(GL_TEXTURE_2D,
				0,
				3,
				texLoader.getImageWidth(),
				texLoader.getImageHeight(),
				0,
				GL_RGB,
				GL_UNSIGNED_BYTE,
				texLoader.getTexture()
				);
	}
}

Metode som laster flere bilder. Metoden tar en parameter, en tabell med filnavn.

public void loadTextures(String[] files) {
	texture = new int[files.length];
	PngTextureLoader texLoader = new PngTextureLoader(gl, glu);
	gl.glGenTextures(files.length, texture);
	for(int i = 0; i < files.length; i++) {
		texLoader.readTexture(files[i]);
		if(texLoader.isOk()) {
		gl.glBindTexture(GL_TEXTURE_2D, texture[i]);
		gl.glTexParameteri(GL_TEXTURE_2D,GL_TEXTURE_MAG_FILTER,GL_NEAREST);
      		gl.glTexParameteri(GL_TEXTURE_2D,GL_TEXTURE_MIN_FILTER,GL_NEAREST);
		gl.glTexParameteri(GL_TEXTURE_2D,GL_TEXTURE_WRAP_S,GL_REPEAT);
      		gl.glTexParameteri(GL_TEXTURE_2D,GL_TEXTURE_WRAP_T,GL_REPEAT);
		gl.glTexEnvf(GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE, GL_MODULATE);
		gl.glTexImage2D(GL_TEXTURE_2D,
					0,
					3,
					texLoader.getImageWidth(),
					texLoader.getImageHeight(),
					0,
					GL_RGB,
					GL_UNSIGNED_BYTE,
					texLoader.getTexture()
					);
		}
	}
}

I tillegg til en av de to metodene som er nevnt over så må en også gjøre følgende. Lage en privat int texture[]. Hvis en bruker den første metoden skal størrelsen være 1. Dersom en bruker den andre metoden skal størrelsen til textures være lik størrelsen til filtabellen. Hva er fordelen med de ulike metodene. Den første metoden egner seg best dersom du kun, skal lese inn 1 tekstur. Hvis du skal bruke flere forskjellige teksturer lønner som regel den andre metoden seg. Dersom du skal bruke flere teksturer og samtidig ha animasjon, vil jeg gå så langt som å si at du MÅ bruke den andre metoden. Dette fordi det sparer deg for unødige i/o operasjoner. I/o operasjoner er det som bruker mest prosessorkraft og vil sette ned hastigheten på animasjonen din betraktelig.

Teksturen til fisken

For fisken min har jeg valgt å lage en tekstur for selve fiskekroppen, en annen for alle finnene og en egen for øyene. Dette fører til at jeg må lese inn minst 3 forskjellige teksturer. Ved å bruke metoden som er forklart ovenfor får jeg lest inn så mange teskturer som er ønskelig. Dette gjorde også at jeg kunne utvide og bruke flere forskjellig teksturer på fisken. Hvordan får man så den rette teksturen til å vise seg på riktig flate. Det er viktig å vite i hvilken rekkefølge man har lest inn teksturene, slik at man kan hente ut teksturen i riktig posisjon. Jeg sørget for at selve fiskestrukturen var lagret først, deretter finnene og til slutt øyet. Koden som henter riktig tekstur fra tabellen min er som følger:

/*	Texture Mapping*/
gl.glBindTexture(GL_TEXTURE_2D, texture[getBodyTexture()]);
gl.glMap2f(GL_MAP2_TEXTURE_COORD_2, 0, 1, 2, 2, 0, 1, 4, 2, getTxtPoints());
gl.glEnable(GL_MAP2_TEXTURE_COORD_2);

I denne kodesnutten er det metoden glBindTexture() som binder en tekstur til bezierflaten. Av andre parameter kan en se at en bruker texture tabellen. Metoden getBodyTexture() returnerer en int som inneholder posisjonen til BodyTexture i tabellen. Metoden glMap2f() sier hvordan texturen skal mappes på bezierflaten. Metoden getTxtPoints() returnerer en tabell som inneholder kontrollpunkter for teksturen. Den siste metoden sørger for at teksturen blir vist i det hele tatt.

Teksturene mine ble laget i adobe photoshop. Jeg har ikke veldig store kunnskaper om adobe photoshop, så teksturene ble nok ikke alltid som jeg håpet på. Og det er nok ganske tidkrevende å få laget en tekstur som man er veldig fornøyd med.

Animasjon

Generelt

Animasjon kan være med å gjøre en ting mer levende og brukes for å se på hvordan enkelte fenomener egentlig oppfører seg i virkeligheten. Animasjon kan være et utslag fra matematiske formler eller fysiske lover. Noen ganger kan animasjonene være av svært liten art.

Animasjon i OpenGL

Det viktigste her er at canvaset ditt er av typen GLAnimCanvas. Et slikt canvas vil stå for gjentakelsene(inkrementeringene) på egenhånd. For å starte prosessen må en kalle canvaset sin start metode. Selve animasjonsprosessen er det lurt å kontrollere i dispaly() metoden, eller i forbindelse med denne.

Fiskens animasjon

Neste hoveddel er realisering av fiskebevegelsene. Men hvordan beveger egentlig en fisk på seg. For å komme seg fremover er fisken nødt til å bruke kroppen, og da primært halen for å kunne skyte fart fremover. Hva slags teknikk fiskene benytter seg av avhenger bl.a av formen til fisken. Det er også verdt å merke seg at rovfisker ofte har mer bevegelige kropper, mens planteetenede fisker har mer funksjonelle bevegelser i forhold til å bevege seg over lengre distanser mest mulig økonomisk. Man har i alt 4 forskjellige hovedmetoder som en fisk kan bevege seg på. De tre første dreier seg om at store deler av kroppen beveger seg for å skape fremdrift, mens den siste metoden bare bruker halen for å få fremdrift.

De tre kroppsbevegelses metodene er:

Anguilliform: gjelder for fisker med lange tynne og smidige(fleksible) kropper, som f.eks en åler og haier. Disse svømmerne bruker typisk hele kroppen for å skape fremdrift.
Carangiform: Fisker som svømmer med bakre del av kroppen og halefinnen. Fremdelen av fisken er statisk. Ca 1/3 av fisken er med på bevegelsen for å skape fremdrift, f.eks makrell og tunfisk.
Subcarangiform: mellomting mellom de to overnevnte eksempel på slike fisker er torsk og trout?. Disse fiskene bruker 2/3 av kroppens lengde for å skape fremdrift og til å svømme med.
I tillegg så har vi en ren oscilliate bevegelse, dette er når fisken kun beveger halen for å skape fremdrift. Ganske vanlig blandt akvariefisker.

bodySwim

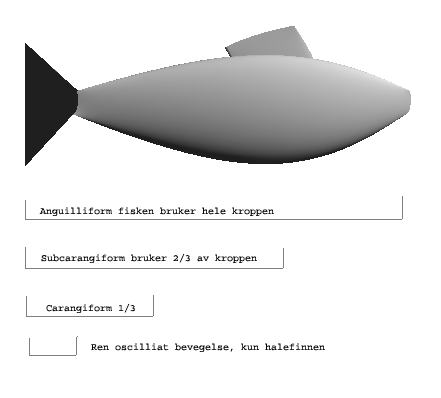
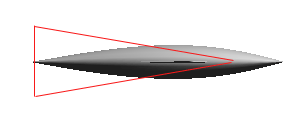
Jeg måtte bestemme meg for hvilken av disse metodene som jeg ville bruke. Jeg kom frem til at den enkleste å implementere kanskje hadde vært ren oscilliat bevegelse, men fisken min så ikke ut som en typisk halefinnefisk. Derfor bestemte jeg at det beste ville være å prøve å få 1/ til 2/3 av kroppen til å bevege seg. For å få bakre del av fisken til å bevege seg, mens fremre del holdt seg statisk, ville det være mest hensikstmessig å bare forandre på z-verdien i enkelte av kontrollpunktene. Som en kan se av figuren under, som er fra xy planet, så var det de punktene i den rosa delen som måtte endres for å få til en bevegelse med bakre del av fisken. Fremre del, altså det gule, ville forbli statisk.

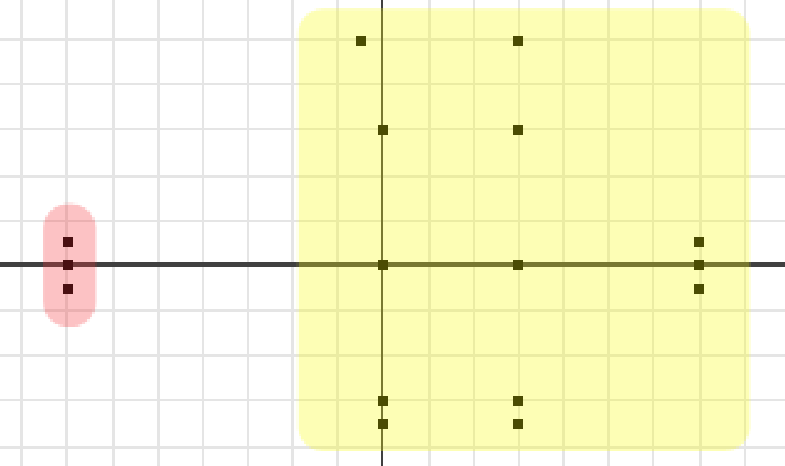
Det jeg ønsket å oppnå med dette var å bevege bakre del, på det ene bildet ser vi maks utslag for halen og hvordan kroppen er i forhold, mens det andre bildet viser en trekant, som gjenspeiler hvordan bevegelsene på fisken stadig blir mindre jo lengre frem på fisken en kommer:

Finnene

Først hadde jeg ikke tenkt så mye på bevegelse av finnene, men det viste seg etterhvert at alle disse også måtte flyttes med den bakre del av fisken. Halefinnen ser jeg for me bare er statisk, derfor blir den tegnet likt hver gang, men flytter bare z punktene. Ryggfinnen og sidefinnene var større utfordringer. Disse måtte følge bevegelsene til resten av fisken, men samtidig så skulle ikke bevegelsen der disse finnen satt være like stor som bevegelsen bakerst på fisken. Se forøvrig illustrasjonen over. Der er det maks utslag helt bakerst, mens det blir gradvis mindre utslag jo lenger frem en kommer. Løsningen ble å bruke mindre forflytninger på disse finnene enn på bakdelen av fisken.

Øyene

Øyet sitter såpass langt fremme på fisken at det ikke er nødvendig å bevege disse i takt med resten av fisken. Disse er derfor statiske.

Løsningen

Nå hadde jeg kommet frem til fornuftige måter å angripe problemet på.

For å få bevegelse i det hele tatt innførte jeg noen variabler. Disse variablene ble så brukt i beveglesene til fisken. Variabelen dt viser hvor mange sekund det skal være mellom hver frame. Framecount teller antall frames. newZ er den nye z verdien som er beregnet og skal tegnes ut. Den boolske variabelen cWise henspeiler på om animasjonen går med eller mot klokken. Den siste boolske verdien bestemmer om fisken skal animeres i det hele tatt.

private double dt = 0.1; // seconds between frames.
private int framecount = 0;
private float newZ = 0.0f;
private boolean cWise = true;
private boolean fishAnimate;

Den lille kodesnutten er ikke nok i seg selv. En må ha en kontrollstruktur og en øking av variabelen newZ og test på endring av retning. I selve display metoden til canvaset la jeg denne koden:

if(fishAnimate) {
	if(newZ > myFish.getMaxSwing())
		cWise = false;
	if(newZ < myFish.getMinSwing())
		cWise = true;
	if(cWise) {
		newZ = newZ + 0.1f;
	} else {
	newZ = newZ - 0.1f;
	}
	// flytt alt du vil flytte med newZ
	myFish.moveFish(newZ);
	myFish.getFishTail().moveTail(newZ);
	myFish.getBackFin().moveBackFin(newZ);
	myFish.getLeftFin().moveSideFin(newZ);
	myFish.getRightFin().moveSideFin(newZ);
}

Den første linjen er bare en if test på om det skal animeres i det hele tatt. getMaxSwing og getMinSwing er to metoder som returnerer maks og min utslag til fiskehalen. Disse verdiene bestemmes av størrelsen til fisken. Er det større fisk, så skal den bruke større halesving ( se forøvrig skalering). De to verdiene maxSwing og minSwing henspeiler på den ytterste posisjonen som halen kan befinne seg i. NewZ verdien vil variere innenfor dette rommet. Dersom en har kommet til en av endene så skal en endre retning, retningen bestemmes av den boolske verdin cWise. Selve flyttingen av fisken skjer i egne metoder. Vi skal se nærmer på den metoden som flytter selve fiskekroppen. Denne metoden ligger i filen Fish.java.

public void moveFish(float newZ) {
	zStart1 = newZ;
	zStart2 = newZ;
	zStart3 = newZ;
	zStart4 = newZ;
	zStart5 = newZ;

	setFishBody();
}

Metoden får inn en newZ verdi og tildeler denne verdien til lokale z varable. Metoden setFishBody lager så nye kontrollpunkter til fiskekroppen. Disse nye kontrollpunktene brukes så igjen når man tegner fisken på nytt. Vi ser at enden av fiskekroppen følger newZ hele tiden, dette fører til at kroppen gjør maks utsving når newZ har størst/minst verdi.

Med ryggfinnen er det litt annerledes. Denne skal ikke skal ha maks utsving og dermed blir move metoden noe annerledes, spesielt med tanke på hvordan nye verdier regnes ut. En kan også se at det er atskillig flere variabler som blir påvirket i denne klassen. Utrekningen av hvert punkt sørger for at utslagene ikke blir så store som de blir helt bakerst på fisken, men at finnen istedet følger bevegelsene til fisken der finnen er plassert.

public void moveBackFin(float newZ) {
	zStart1 = newZ/5.0f; zCtrp1_1 = newZ/5.0f; zCtrp2_1 = newZ/5.0f; zEnd1 = newZ/5.0f;
	zStart2 = newZ/7.0f; zCtrp1_2 = newZ/7.0f; zCtrp2_2 = newZ/7.0f; zEnd2 = newZ/7.0f;
	zStart3 = newZ/9.0f; zCtrp1_3 = newZ/9.0f; zCtrp2_3 = newZ/9.0f; zEnd3 = newZ/9.0f;
	zStart7 = newZ/9.0f; zCtrp1_7 = newZ/9.0f; zCtrp2_7 = newZ/9.0f; zEnd7 = newZ/9.0f;
	zStart8 = newZ/7.0f; zCtrp1_8 = newZ/7.0f; zCtrp2_8 = newZ/7.0f; zEnd8 = newZ/7.0f;
	zStart9 = newZ/5.0f;
	setBackFinCoord();
}

Alle klasser som innholder bevegelse har sin egen move metode. Utslaget i move metoden gjenspeiles av objektets plassering på fiskekroppen, på den måten sikrer man fine glatte og naturlige bevegelser.

Frames

Generelt

Frames kan brukes for å vise et bestemt bevegelsesmønster. Det kan være en ting som går i sirkel, noe som beveger seg opp og ned. Mens animasjoner, mer er begrenset til bevegelser på selve objektet, f.eks en arm eller hodet, så er frames mer myntet på å få hele objektet til å bevege seg i et mønster. Mønsteret kan være forhåndsbestemt, og det kan gjøres tilfeldig. Modulen frames omtaler to måter å realisere bruken av frames på. Den ene måten er ved å bruke en spiral, mens den andre er ved å bruke en bezierkurve.

Uansett hva slags måte en realiserer problemet på så er det enkelte ting som må gjøres. Det er å finne den riktige retningen til objektet i forhold til den kurven som objektet skal følge. Men det finnes en løsning på problemet. Løsningen er delt opp i følgende steg: bezierRetn

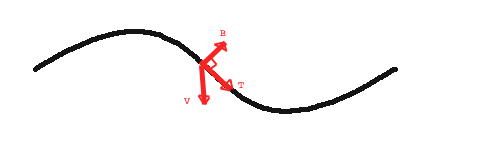
Bestem en vektor T i det nye systemet.
Velg en vektor V , som ikke er kolineær med T.
Bestem den andre aksen B = T*V
Bestem den tredje aksen N = T*B
Normaliser T, B, N
En kan nå formulere en matrise M som realiserer den ønskede transformasjonen. M kan skrives M = |T B N C |. Alle vektorene er beregnet for en bestemt t-verdi.

For å simplifisere veldig så vil dette si at dersom man har en formel for en rett linje:

F(t) = t + 1

I dette tilfellet så vil matrisen gjelde for hver verdi av t. En t verdi 1 vil gi en egen matrise M, mens en t verdi 2 vil gi en annen matrise osv. Den deriverte i dette tilfellet vil være 1 som antyder at stigningen er konstant 1.Den dobbeltderiverte skal angi krummingen på kurven etter som dette er en rett linje har kurven ingen krumming, dermed blir det riktig at den dobbeltderiverte er 0.

Når det gjelder bezierkurver så foreslår Hill at man skal bruke den deriverte i stedet for T og den dobbelderiverte istedet for vektoren V. Ved en bezierkurve så vil dette føre til problemer, spesielt dersom man har en retningsforandring mitt på kurven. Så i bezierkurve tilfellet kan det være tryggere å bruke en annen vektor.

Fiskens bevegelser

Hvordan kan en så bruke frames for å realisere en fisk sine bevegelser? Det jeg ønsker å oppnå er at fisken beveger seg over skjermen i et mønster. Tanken min er at jeg skal lage en bezierkurve som fisken min skal bevege seg langs. Fisken skal følge denne kurven som en prametrisk funksjon og skrives ut for hvert punkt langs kurven. Selve bezierkurven kommer til å være statisk, for enkelthets skyld. Antall punkt på kurven gjenspeiler hvor fort fisken svømmer. Har du mange punkter svømmer den sent, har du færre punkter svømmer fisken raskere. Rent grafisk kan dette vises som følger:

parameterKurve

Den første bezierKurven vil her kun ha 6 stopp, dette vil føre til at fisken, eller objektet vil svømme veldig fort. Mens den andre bezier kurven har markant flere punkter. Her vil fisken, eller objektet bevege seg mye saktere. Ved å øke tettheten på punktene så senker man altså farten på objektet, men får også en mer flytende bevegelse. Hva som er det riktige antall "stopp" avhenger av lengden på den kurven som skal brukes, men også av hvor raskt fisken skal bevege seg. Her vil jeg si at det ikke er noe entydig svar, annet en at det bare er å prøve seg frem.

Løsningen

For å kunne løse problemet på en tilfredsstillende måte så fant jeg det mest fornuftig å lage to hjelpeklasser. Den ene var en en 3D vektor klasse som tar vare på x, y og z- verdien til en vektor. I tillegg så ville jeg ha en bezierkurve klasse som tok vare på all informasjonen om selve bezierkurven. Denne hjelpeklassen skulle regne ut både den deriverte og den dobbeltderiverte. Alt som hadde med OpenGL ble lagt i canvaset.

Det som ligger i en egen metode i canvaset er koden som følger under. Denne koden er avhandlet av koden som finnes i modulen Frames, men den er skrevet om til java og tilpasset vector og bezierkurve klassene. BezCurve.getOrder() er så mange verdier som er regnet ut langs bezierkurven. En kan si det slik at det er dette som avgjør hvor tett objektet skal tegnes på bezierkurven.

while(ix < bezCurve.getOrder()) {
	//  T vector
	T = new Vector3D(bezCurve.getDBezAtPos(ix, 0), bezCurve.getDBezAtPos(ix, 1),bezCurve.getDBezAtPos(ix, 2));
	T.normalize();

	// B vector
	B = new Vector3D(bezCurve.getDBezAtPos(ix, 0), bezCurve.getDBezAtPos(ix, 1),bezCurve.getDBezAtPos(ix, 2));
	//B.cross(bezCurve.getDDBezAtPos(ix, 0), bezCurve.getDDBezAtPos(ix, 1),bezCurve.getDDBezAtPos(ix, 2));
	B.cross(0.0f,0.0f,1.0f);
	B.normalize();

	// N vector
	N = new Vector3D(B.getX(),B.getY(),B.getZ());
	N.cross(T);  // and it is normalized since B and T are

	// C vector
	C = new Vector3D(bezCurve.getBezAtPos(ix, 0), bezCurve.getBezAtPos(ix, 1),bezCurve.getBezAtPos(ix, 2));

	// The Matrix M
	float M[]={
			N.getX(),N.getY(),N.getZ(),0.0f,
			B.getX(),B.getY(),B.getZ(),0.0f,
			T.getX(),T.getY(),T.getZ(),0.0f,
			C.getX(),C.getY(),C.getZ(),1.0f
			};

	gl.glPushMatrix();

	//multiply our newly made Frenet matrix to OpenGLs current matrix
	gl.glMultMatrixf(M);


	/*****************************
	**
	** Vectors and stuff done, we are ready to draw.
	**
	*********************************/

	gl.glPopMatrix();

	ix++;
}

BezierCurve klassen og Vector3D klassen har begge get og set metoder, spesielt get metodene blir brukt flittig i kodebiten over. Tabellene som verdiene hentes fra er store tabeller som opprettes i BezierCurve klassen.

Det er kanskje ikke så lett å forstå alt koden, men i bunn og grunn så er det bare en gjennomgang av de punktene som ble nevnt tidligere, vi kan sette det opp på ny

Bestem en vektor T i det nye systemet.

T = new Vector3D(bezCurve.getDBezAtPos(ix, 0), bezCurve.getDBezAtPos(ix, 1),bezCurve.getDBezAtPos(ix, 2));

Velg en vektor V , som ikke er kolineær med T.
```
0.0f,0.0f,1.0f
```

Bestem den andre aksen B = T*V
Først vektoren B:

B = new Vector3D(bezCurve.getDBezAtPos(ix, 0), bezCurve.getDBezAtPos(ix, 1),bezCurve.getDBezAtPos(ix, 2));

så multiplisere denne med V

B.cross(0.0f,0.0f,1.0f);

Bestem den tredje aksen N = T*B
Først lage N lik B
```
N = new Vector3D(B.getX(),B.getY(),B.getZ());
```
så multiplisere denne med T
```
N.cross(T);
```
Normaliser T, B, N
```
T.normalize(); B.normalize();
```
Ettersom vi normaliserer disser før vi bruker de i utrekning, så er N automatisk normalisert.

En kan nå formulere en matrise M som realiserer den ønskede transformasjonen. M kan skrives M = |T B N C |. Alle vektorene er beregnet for en bestemt t-verdi.

float M[]={
			N.getX(),N.getY(),N.getZ(),0.0f,
			B.getX(),B.getY(),B.getZ(),0.0f,
			T.getX(),T.getY(),T.getZ(),0.0f,
			C.getX(),C.getY(),C.getZ(),1.0f
			};

Vi skal også ta en titt på koden i Vector3D klassen for å se hva metoden normalize gjør med vectoren. Det denne metoden gjør er å regne ut lengden til en vector. Deretter deler den koordinatene på lengden

public void normalize() {
	float l = (float)Math.sqrt(x * x + y * y + z * z);
	x = x/l;
	y = y/l;
	z = z/l;
}

Når vi så har regnet ut alle verdiene vi trenger så blir neste steg er å få tegnet ut objektet, eller i vårt tilfelle fisken. Dette er løst ved å lage en variabel showix. Denne variabelen løper langs bezierkurven, og øker med 1 steg helt til den kommer til enden, da minsker den med 1 for hver iterasjon. Hvor mange steg showix skal gå i hver retning er det en egen variabel som bestemmer. Variabelen order i klassen BezierCurve anngir hvor mange steg som skal tas langs bezierkurven fra den ene enden til den andre. Denne variablene sette når en oppretter et objekt av BezierCurve. I mitt tilfelle så har jeg eksperimentert med mellom 200 og 400 steg. Selve uttegning av fisken på hvert steg er det metoden makeFish() som står for.

if(fishSwim) {
	if(showix==bezCurve.getOrder())
		stepix=-1;
	else if(showix==0)
		stepix=1;
	showix += stepix;
}

if( showix == ix) {
	if(stepix == -1) {
		gl.glRotatef(180, 0.0f, 1.0f, 0.0f);
		makeFish();
	} else
		makeFish();
	}

Foreløpig er bezierkurven min statisk, men jeg har implementert en move metode som beveger bezierkurven også, dersom en lager en fiskestim, eller et akvarium, så kan det være lurt å tilegne hver fisk sin egen bezierkurve og få fisken til å bevege seg langs denne. Eventuelt lage en fiskestim, der alle fiskene beveger seg langs samme bezierkurve som en stor enhet. Eller mulig med en fiskekrok som kommer ned i vannet, en bezierkurve som beveger seg, og ved hjelp av hit detection se om fisken treffer kroken, og dermed blir dratt på land.

Tåke

Generelt

Tåke er et enkelt verktøy for å skape ekstra effekter til miljøet som objektene befinner seg i.

Tåke er enkelt og veldig rett frem å implementere. Det viktigste å være var over er at bakgrunnsfargen og tåken har samme farge, dette for å få best mulig effekt ut av tåken. Kode eksempel på å implementere tåke:

	gl.glEnable(GL_FOG);
	float fogColor[] = { 0.5f, 0.6f, 1.0f, 1.0f };
	gl.glFogfv(GL_FOG_COLOR, fogColor);
	gl.glFogf(GL_FOG_START, 30.0f);
	gl.glFogf(GL_FOG_END, 50.50f);
	gl.glFogi(GL_FOG_MODE, GL_LINEAR);

Den første metoden enabler tåken. fogColor er en variabel for å sette fargen på tåken, det er viktig at den er identisk med bakgrunnsfargen for best resultat. De to neste metodene sier hvor tåken skal starte og slutte. Det er viktig at disse får riktige verdier. Er tåken for langt fremme, ser du f.eks ingenting av bildet ditt. Er tåken for langt bak vil du ikke ha noe effekt av den i det hele tatt. Den siste metoden sier bare noe om hva slags type tåke det er snakk om.

Vannet

Ettersom fisker lever i vann så tenkte jeg at det var artig å lage et miljø rundt fisken som kunne minne om vann. En veldig lett måte å skape følelsen av vann er å bruke tåke. Det var spesielt ønskelig at tåken var på en slik måte at når fisken min svmøte så ville den gradvis svømme lenger inn i tåka(vannet). På bildene under så er det til venstre med tåke, mens det til høyre er uten.

Mulige utvidelser

Lage flere samtidige fisker
Lage et akvarium
Legge til en sandbunn med dyreliv

Lest og lagd

Moduler

Bezier-kurven
Frames
Bilde bok, spesielt vedrørende tekstur og bezierflater.
Monster

Javakode

FishWorld.java
FishGLCanvas.java
Fish.java
Tail.java
BackFin.java
LeftSideFin.java
RightSideFin.java
Eye.java
BezierCurve.java
Vector3D.java

Alle filene zippet

fishProject.zip

Referanser

The OpenGL Programming Guide, 6 editionDave Schreiner, Mason Woo,Jackie Neider,Tom Davies2007Addison-Wesley Professional0321481003www.opengl.org/documentation/red_book/14-03-2010

Computer Graphics Using OpenGL, 3nd editionF.S. Hill, S.M Kelly2001Prentice Hall0131496700