Blekksprut

[Tekstur]

For prinsippene og teorien bak bezierkurver og -flater, nøyer jeg meg med å henvise til modulene Bezier og Flater, siden jeg ikke tror at jeg vil klare å gjøre store forbedringer i måten å forklare dette på. Det jeg derimot vil gå inn på i dette avsnittet er hvordan jeg har brukt bezierflater for å modellere hodet og øynene på blekkspruten min.

For å lage bezierflaten til blekksprutens hode, tok jeg utgangspunkt i modulen Blending og den flaten som er brukt til å modellere timeglasset der. Dette var et naturlig utgangspunkt siden timeglasset har løst problemet med å få flaten rund på en utmerket måte, og det var lett å tilpasse kontrollpunktene for å modellere hodet.

på bildet til venstre ser du at aksesystemet til blekkspruten er slik at hodet "står" på origo, det er altså plassert slik at origo ligger midt på, i hodets underkant. Hodet er hult, men hulrommet blir dekket av armene. på bildet er aksene er farget som følger: rød X-akse, grønn Y-akse og blå Z-akse. Positiv X-akse peker vannrett til høyre, positiv Y-akse er rett opp og positiv Z-akse er rett mot deg.

En bezierflate er en flate som er bygd opp av bezierkurver i begge retninger. Altså trengs det en matrisearray med kontrollpunkter. Kontrollpunktene til blekksprutens bezierflater finnes i klassene Head.java og Eye.java. i denne matrisearrayen er punktene organisert slik at de blir separert horisontalt og vertikalt etter hvor mange punkter det er oppgitt at flaten skal ha i hver retning.

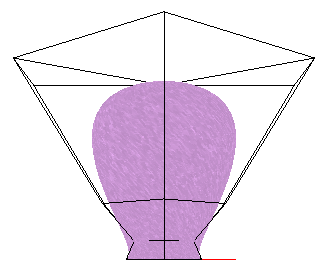
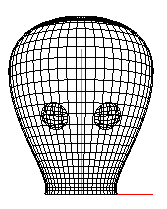
Her er forsiden av blekksprutens hode tegnet med tilhørende kontrollpunkter, for å syneliggjøre hvilken effekt de forskjellige kontrollpunktene har på flatens fasong. Koden for å tegne linjene mellom kontrollpunktene har jeg lånt og tilpasset fra modulen Blending som igjen har lånt den fra Børres modul Trampoline.

For å forklare veien fra matrisen med kontrollpunkter til ferdig tegnet bezierflate, velger jeg å bruke øyets kontrollpunkter som eksempel siden det har færrest punkter. Øyet blir her tegnet "liggende" i origo, for så å roteres på plass. Slik kan de samme kontrollpunktene lett brukes til å modellere både høyre og venstre øye med de samme verdiene for rotering og flytting, bare omvendt om y-aksen.

// Antall kontrollpunkter i hver retning
int UN =4; // langs z-aksen
int VN =4; // langs x-aksen

// Matrisearray med alle kontrollpunktene til øyet
float ctrPoints[] =  {
  //un 1
  -0.065f,  0.025f, -0.06f,   //nederst til venstre på øyet, vn1
  -0.025f,  0.025f, -0.1f,    //vn 2
  0.025f,   0.025f, -0.1f,    //vn 3
  0.065f,   0.025f, -0.06f    //vn 4
  ,
  //un 2
  -0.1f,    0.025f, -0.045f,  //vn1
  -0.045f,  -0.05f, -0.045f,  //vn2
  0.045f,   -0.05f, -0.045f,  //vn3
  0.1f,   0.025f, -0.045f     //vn4
  ,
  //un 3
  -0.1f,    0.025f, 0.045f,   //vn1
  -0.045f,  -0.05f, 0.045f,   //vn2
  0.045f,   -0.05f, 0.045f,   //vn3
  0.1f,   0.025f, 0.045f      //vn4
  ,
  //un 4
  -0.065f,  0.025f, 0.06f,    //øverst til venstre på øyet, vn1
  -0.025f,  0.025f, 0.1f,     //vn2
  0.025f,   0.025f, 0.1f,     //vn3
  0.065f,   0.025f, 0.06f     //vn4
};
    

Hvert kontrollpunkt består av tre koordinater (x, y, z), og hver kurve består av fire kontrollpunkter (i begge retninger). Blokkene på fire og fire punkter her, beskriver kurvene langs x-aksen og begynner med den med lavest z-verdi (bakerst), mens punktene merket vn1 beskriver den kurven som er lengst til venstre langs z-aksen, de merket med vn2 den neste osv.

Selve uttegningen av bezierflaten skjer ved hjelp av flere gl-funksjoner. Jeg presenterer dem her i tur og orden, med forklaring på funksjon og parametre mellom:

gl.glMap2f(GL_MAP2_VERTEX_3,
           0.0f, 1.0f, 3,
           eye.getUN(), 0.0f, 1.0f,
           3*eye.getUN(), eye.getVN(), eye.getCtrPoints());
    

Denne linjen forteller OpenGL hvor matrisearrayen skal hentes fra, og hvordan den er bygd opp. Utfra dette settes parametrene for bezierflaten.

1. GL_MAP2_VERTEX_3
   Hvert kontrollpunkt oppgitt i matrisen består av tre koordinater. Genererer glVertex3()-kommandoer når flaten evalueres.
2. 0.0f
   Minste verdi av u.
3. 1.0f
   Høyeste verdi av u.
4. 3
   Antall verdier mellom hvert punkt i u-retningen.
5. eye.getUN()
   Antall kontrollpunkter i u-retningen (i dette tilfellet UN = 4).
6. 0.0f
   Minste verdi av v.
7. 1.0f
   Høyeste verdi av v.
8. 3*eye.getUN()
   Antall verdier mellom hvert punkt i v-retningen.
9. eye.getVN()
   Antall kontrollpunkter i v-retningen (i dette tilfellet VN = 4).
10. eye.getCtrPoints()
    Selve matrisearrayen med kontrollpunkter.

gl.glEnable(GL_MAP2_VERTEX_3);
    

Aktiviserer evaluering av todimensjonale "vertex'er" med tre koordinater.

gl.glMapGrid2f(7, 0.0f, 1.0f, 7, 0.0f, 1.0f);
    

Når en bezierflate evalueres genereres et rutenett med et gitt antall ruter i begge retninger. Flaten kan så tegnes som punkt, linjer eller fylte ruter utfra dette rutenettet. Parametrene til glMapGrid2f() representerer antallet ruter i begge retninger, samt hvor stor del av flaten som skal dekkes. De tre første gjelder i u-retningen og sier at flaten skal ha 7 ruter, og at den skal dekke hele området som u spenner over (fra 0.0 til 1.0). De tre neste er tilsvarende verdier for v-retningen.

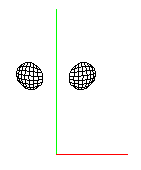
Man kan utforme rutenettet slik at det har ulikt antall ruter på ulike deler av flaten, noe som kan være nyttig, siden flaten blir tyngre å laste jo flere ruter som skal genereres. på bildet til venstre er flaten for blekksprutens øyne tegnet med linjer, og rotert på plass til henholdsvis venstre og høyre øye. Jeg har brukt samme antall ruter over hele flaten, både på øynene og på hodet.

gl.glEvalMesh2(GL_FILL, 0, 7, 0, 7);
    

Her tegnes flaten. Denne metoden kjøres på bakgrunn av den mappingen som ble gjort i glMapGrid2f()-funksjonen, og sier at flaten skal tegnes med 7 ruter i begge retninger, og rutene skal fylles. For å få linjer er det bare å endre første parameter til GL_LINE.

Eventuell rotering, flytting og skalering må gjøres før flaten tegnes, altså før glEvalMesh2() kalles.

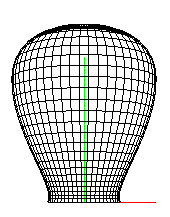
Blekksprutens hode er en større flate og må derfor ha flere ruter for å bli jevn og pen. i tillegg skal hodet være rundt og symmetrisk om y-aksen. Istedenfor å gjøre dette ved å lage èn rund flate, noe som vil kreve flere ressurser til lagring av kontrollpunkter og oppbygning av flaten, lagres punkter for halve flaten. Så når flaten skal tegnes, tegnes den først en gang før vi roterer 180 grader og tegner flaten en gang til.

gl.glMapGrid2f(25, 0.0f, 1.0f, 25, 0.0f, 1.0f);
gl.glEvalMesh2(GL_FILL, 0, 25, 0, 25);
gl.glRotatef(180, 0, 1, 0);
gl.glEvalMesh2(GL_FILL, 0, 25, 0, 25);
    

Det første bildet under viser rutenettene for hodet og øynene satt sammen. Siden hodet har en fasong som er avrundet i begge retninger viste det seg å være vanskelig å få lagt øye-flaten helt inntil uten at det blir "glipper" mellom hodet og øye på enkelte steder. For å unngå dette valgte jeg å trekke øyeflaten litt inn i hodet, slik at alle kanter er tette.

Det andre bildet viser flatene fylt med tekstur, og i neste avsnitt forklarer jeg i korte trekk hvordan jeg har lagt tekstur på bezierflatene.

Jeg valgte å lagre mine teksturfiler i png-format, og må derfor bruke PngTekstureLoader for å laste teksturene. Bilder som skal brukes som teksturer må ha en størrelse på 2^n X 2^m. Mine teksturer for øyne og armer er 64 X 64, mens den for hodet er 256 X 256.

Følgende kode benyttes for å laste teksturer:

public void textures(String file) {
  // Bruker .png bilder derfor PngTextureLoader
  PngTextureLoader txtLoader = new PngTextureLoader(gl, glu);
    txtLoader.readTexture(file);
  if(txtLoader.isOk()) {
    // Genererer tekstur og legger den i arrayen
    gl.glGenTextures(1, texName);
    gl.glBindTexture(GL_TEXTURE_2D, texName[0]);
    // Her lages teksturen, gir høyde, bredde og annen informasjon om bildet
    gl.glTexImage2D(GL_TEXTURE_2D, 0, 3,
        txtLoader.getImageWidth(),
        txtLoader.getImageHeight(),
        0, GL_RGB, GL_UNSIGNED_BYTE,
        txtLoader.getTexture());
  }
}
    

1. PngTextureLoader brukes til å lese bildefila og hente teksturen.
2. glGenTextures returnerer en ledig identifikator for teksturen.
3. glBindTexture genererer et nytt teksturobjekt med den gitte identifikator.
4. glTexImage2D lager teksturen.
   • GL_TEXTURE_2D sier at bildefila er todimensjonal.
   • 0 sier at bildefila bare har en oppløsning.
   • 3 sier at av R,G,B og a bruker vi R, G og B.
   • txtLoader.getImageWidth() henter bredden på bildet.
   • txtLoader.getImageHeight() henter høyden på bildet.
   • 0 sier at vi ikke vil ha ramme rundt teksturen.
   • GL_RGB og GL_UNSIGNED_BYTE sier hvilket format og hvilken type data bildet inneholder.
   • txtLoader.getTexture() henter bildet som tekstur.

gl.glEnable(GL_TEXTURE_2D);
    

Aktiviserer bruk av teksturer. Denne må aktiviseres og deaktiveres for hver gang du bruker en tekstur, ellers vil alle flater og kurver som tegnes bli tegnet med den første teksturen som aktiviseres.

// Legger teksturen utover hele flaten
gl.glTexParameteri(GL_TEXTURE_2D,GL_TEXTURE_WRAP_S,GL_CLAMP);
gl.glTexParameteri(GL_TEXTURE_2D,GL_TEXTURE_WRAP_T,GL_CLAMP);

// Hvordan teksturen skal strekkes
gl.glTexParameteri(GL_TEXTURE_2D,GL_TEXTURE_MAG_FILTER,GL_NEAREST);
gl.glTexParameteri(GL_TEXTURE_2D,GL_TEXTURE_MIN_FILTER,GL_NEAREST);

// Bytter ut fargen med teksturen
gl.glTexEnvf(GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE, GL_REPLACE);

// Setter teksturens koordinater
gl.glMap2f(GL_MAP2_TEXTURE_COORD_2,
      0,1,2,2,
      0,1,4,2,textPoints);

// Aktiviserer koordinat-mappingen
gl.glEnable(GL_MAP2_TEXTURE_COORD_2);

/*** Tegne bezierflaten ***/
    

Det jeg slet mest med når det gjaldt teksturer var å få til et bilde som fikk frem dybdefølelsen i modellen. Bildet lengst til venstre viser teksturen som er brukt på blekksprutens armer. Her har jeg valgt å gjøre bildet lysere mot midten, og dette medfører at armene ser ut som de er belyst ovenfra (se Resultat). For teksturen på hodet (det andre bildet viser et utsnitt av denne) var ikke dette like enkelt. På grunn av dette valgte jeg å lage denne teksturen med samme farge over hele. Som du kan se på screenshots'ene Bezier-avsnittet medfører dette at hodet ser litt flatt ut.

Øyets tekstur har jeg lånt fra modulen Monster. Siden denne teksturen har en lyseffekt i tillegg til at den har mange runde linjer, kommer kurvene i bezierflaten frem og resultatet blir derfor bedre enn med hode-teksturen.

Frames benyttes dersom vi har en eller annen parametrisk kurve, og ønsker å tegne en figur som beveger seg langs kurven, eller mange figurer av samme type som ligger langs kurven.

i mitt tilfelle bruker jeg frames til å tegne armene på blekkspruten. Jeg lager fasongen på armene ved hjelp av bezierkurver, og lager tykkelsen ved hjelp av små sylindere som ligger langs kurven.

Bildet under viser et eksempel på en bezierkurve brukt til å fremstille en blekksprutarm.

while( t < t_max) {
  glPushMatrix();
  glTranslate(Cx(t),Cy(t),Cz(t));
  < tegn figur >
  glPopMatrix();
  t += t_step;
}
    

Kodesnutten over er hentet fra modulen Frames, og gir en løsning på dette problemet, men denne løsningen er ikke fullstendig dersom figurens orientering på kurven er relevant. Da må vi innføre et steg < roter figuren på plass > før vi tegner figuren, og dette er ikke helt trivielt.

Perler uten rotering		Bokser uten rotering		Bokser med rotering

Som du kan se på det første bildet over, går det greit å tegne figuren uten å rotere så lenge figuren har en fasong som gjør at det ikke spiller noen rolle hvilken retning den tegnes. på bildet i midten ser du at det blir rart når det som tegnes er bokser og alle boksene har samme retning. på det siste bildet er aksene rotert, og boksene følger retningen til kurven. på armene på blekkspruten min er det sylindere som følger kurven. Sylindere har topp og bunn, og jeg måtte derfor rotere aksene for å få en glatt og fin overflate.

Det man gjør for å rotere aksene er å sette opp et nytt aksesystem som gjelder bare for den enkelte figur som tegnes. Måten vi setter opp dette aksesystemet på er ved først å velge en vektor, T, som skal utgjøre den ene aksen i det nye systemet. For å få rekken med figurer til å følge kurven, er det naturlig at den ene aksen følger kurven, og vi setter derfor T til å være kurvens deriverte ved det punktet der vi begynner å tegne hver figur.

Nå har vi èn akse i det nye systemet, og det vi trenger er to til. Disse to må være normaler både til den første aksen og til hverandre. Det vi gjør for å finne disse er at vi velger en vektor, V, kryssproduktet av V og T utgjør B, og så finner vi den siste aksen, N, ved kryssproduktet av T og B.

Det eneste vi har igjen å gjøre er altså å velge V. Som du kan lese i modulen Frames er det eneste formelle kravet vi stiller til V at den ikke faller sammen med (er colineær med) T. Hvis denne betingelsen er oppfylt vet vi at kryssproduktet av V og T gir oss en vektor som er normal på T (og V). Vi kan altså i prinsippet velge en hvilken som helst vektor. F.S. Hill foreslår i boka "Computer Graphics using OpenGL" å bruke den dobbeltderiverte som V, men dette ble problematisk da jeg skulle lage armene på blekkspruten, fordi når bezierkurven har krumninger i flere retninger, endrer den dobbeltderiverte fortegn, og aksene "vrenges" til motsatt side av kurven

Bildene over viser resultatet da jeg prøvde å sette opp et aksesystem med den dobbeltderiverte som V for den første av blekksprutens armer. Et annet alternativ er å ha en fastsatt vektor som V, men da må man passe på at den aldri faller sammen med T. i mitt prosjekt valgte jeg V = (0.0, 0.0, 1.0), og resultatet kan du se under

Når vi har bestemt aksene, T, B og N, i det nye systemet, må de normaliseres slik at de får lengde 1, for når vi skal sette opp transformasjonsmatrisen må vi arbeide med enhetsvektorene i det nye systemet. Selve normaliseringen gjøres på følgende måte: For en vektor a finner vi den normaliserte ved AN=a/|a|, der |a| er (a0*a0+a1*a1+a2*a2+a3*a3)^1/2.

Når vi har funnet enhetsvektorene, kan vi sette opp følgende matrise som realiserer transformasjonen: M = |T B N C|, der C er selve kurven. Utskrevet ser matrisen sånn ut:

    |t0 b0 n0 c0|
    |t1 b1 n1 c1|
M = |t2 b2 n2 c2|
    |t3 b3 n3 c3|
    

Denne matrisen multipliseres så med den matrisen vi allerede har, vi kan tegne hva vi vil, og figurene vil følge kurven.

Da jeg skulle lage armene begynte jeg med den bezierkurven som du ser på det første bildet i dette avsnittet. Jeg satte opp matriser for å holde ligningene som brukes for å beregne punktene til kurven og den deriverte, og matriser for å holde de beregnete punktene. Følgende kode setter opp matrisene og beregner kurvenes punkter:

/** Satt i konstruktøren */
int MAX_STEPS = 80;         // Antall punkter pr kurve (og sylindere pr arm)

float btab[][] = new float[4][MAX_STEPS]; // ligningene for å regne ut bezierfunksjonen
float d_btab[][] = new float[4][MAX_STEPS]; // ligningene for å regne ut den deriverte

float bez[][] = new float[MAX_STEPS][3];  // verdiene til bezierfunksjonen
float d_bez[][] = new float[MAX_STEPS][3];  // verdiene til den deriverte

// Setter opp matrisene som holder ligningene for å regne ut kurven
int tix=0;
while(tix < MAX_STEPS) {
  float t=(1.0f/(1.0f*MAX_STEPS))*(1.0f*tix);
  btab[0][tix]=(1-t)*(1-t)*(1-t);
  btab[1][tix]=3.0f*t*(1-t)*(1-t);
  btab[2][tix]=3.0f*t*t*(1-t);
  btab[3][tix]=t*t*t;
  tix++;
}

// Setter opp matrisene som holder ligningene for å regne ut kurven til den deriverte
tix=0;
while(tix < MAX_STEPS) {
  float t=(1.0f/(1.0f*MAX_STEPS))*(1.0f*tix);
  d_btab[0][tix]=-3.0f*t*t+6.0f*t-3.0f;
  d_btab[1][tix]=9.0f*t*t-12.0f*t+3.0f;
  d_btab[2][tix]=-9.0f*t*t+6.0f*t;
  d_btab[3][tix]=3.0f*t*t;
  tix++;
}

g_vStartPoint = new CVector3(-2, 0, 0);     // Bezierkurvens startpunkt
g_vControlPoint1 = new CVector3(-1.5f, -0.5f, 0); // Det første kontrollpunktet
g_vControlPoint2 = new CVector3(-1, 0.125f, 0);   // Det andre kontrollpunktet
g_vEndPoint = new CVector3(0, 0, 0);      // Bezierkurvens endepunkt

// Kaller metodene som setter opp matrisene som holder punktene til kurven og den deriverte
makeBezier(g_vStartPoint, g_vControlPoint1, g_vControlPoint2, g_vEndPoint);
make_d_Bezier(g_vStartPoint, g_vControlPoint1, g_vControlPoint2, g_vEndPoint);


/** Metoder for å beregne punktene til kurven og den deriverte */

// Setter opp matrisen som holder punktene til bezierfunksjonen
private void makeBezier(CVector3 p0, CVector3 p1, CVector3 p2, CVector3 p3) {
  int ix = 0;
  while(ix < MAX_STEPS) {
    bez[ix][0]=p0.x*btab[0][ix]+p1.x*btab[1][ix]+p2.x*btab[2][ix]+p3.x*btab[3][ix];
    bez[ix][1]=p0.y*btab[0][ix]+p1.y*btab[1][ix]+p2.y*btab[2][ix]+p3.y*btab[3][ix];
    bez[ix][2]=p0.z*btab[0][ix]+p1.z*btab[1][ix]+p2.z*btab[2][ix]+p3.z*btab[3][ix];
    ix++;
  }
}

// Setter opp matrisen som holder punktene til den deriverte
private void make_d_Bezier(CVector3 p0, CVector3 p1, CVector3 p2, CVector3 p3) {
  int ix = 0;
  while(ix < MAX_STEPS) {
    d_bez[ix][0]=p0.x*d_btab[0][ix]+p1.x*d_btab[1][ix]+p2.x*d_btab[2][ix]+p3.x*d_btab[3][ix];
    d_bez[ix][1]=p0.y*d_btab[0][ix]+p1.y*d_btab[1][ix]+p2.y*d_btab[2][ix]+p3.y*d_btab[3][ix];
    d_bez[ix][2]=p0.z*d_btab[0][ix]+p1.z*d_btab[1][ix]+p2.z*d_btab[2][ix]+p3.z*d_btab[3][ix];
    ix++;
  }
}
    

Nå har jeg altså en bezierkurve, og matriser med alle nødvendige punkter ferdig beregnet. Neste skritt blir å sette opp det roterte aksesystemet. Følgende kode gjør det:

int ix=0;
cylRad = 0.0225f;

while(ix < MAX_STEPS) {
  // Bruker den deriverte, som ligger langs kurven, som tangent
  CVector3 T = new CVector3(d_bez[ix][0],d_bez[ix][1],d_bez[ix][2]);
  T.normalize(); // Normaliserer T

  /* Finner en vektor ulik T, kan ikke bruke den dobbeltderiverte, fordi der kurven
     endrer retning, og aksene snur, mangler en sylinder og blekkspruten ser ut som
     den har t-skjorte på... */
  CVector3 B = new CVector3(d_bez[ix][0],d_bez[ix][1],d_bez[ix][2]); // B = T
  B.cross(0.0f,0.0f,1.0f); // B = T x (0.0, 0.0, 1.0)
  B.normalize(); // Normaliserer B

  CVector3 N = new CVector3(B.x,B.y,B.z); // N = B
  N.cross(T);  // N = B x T -> N er normalisert siden B og T er det

  // C er kurven selv
  CVector3 C = new CVector3(bez[ix][0],bez[ix][1],bez[ix][2]);

  float M[] = {
    N.x,N.y,N.z,0,
    B.x,B.y,B.z,0,
    T.x,T.y,T.z,0,
    C.x,C.y,C.z,1
  };

  // Tar vare på den matrisen som allerede eksisterer
  gl.glPushMatrix();

  // Multipliserer Frenet matrisen til OpenGLs matrise
  gl.glMultMatrixf(M);

  // Klar til å tegne
  long glCyl = glu.gluNewQuadric();

  if(ix == 0){
    // Tegner en liten kule i enden av hver arm fordi de er hule
    long glSphere = glu.gluNewQuadric();
    glu.gluQuadricTexture(glSphere,true);
    glu.gluSphere(glSphere,cylRad,20,20);
  }
  glu.gluQuadricTexture(glCyl,true);
  glu.gluCylinder(glCyl,cylRad,cylRad*incFac,(2/MAX_STEPS)+0.075,15,1);
  glu.gluDeleteQuadric(glCyl);
  gl.glPopMatrix();

  // neste t-posisjon
  ix++;

  // øker radius på den neste sylinderen
  // 1.0225 er faktor for armene i utgangs- og flyteposisjon
  // 1.025 er faktor for armene i svømmeposisjon
  cylRad *= incFac;
}
    

Etter at punktene til bezierkurven er beregnet og aksesystemet er satt opp, kan vi begynne å tegne sylindere for å gjøre armen rund. Antallet punkter på kurven er satt til 80, og dette blir også antallet sylindere langs kurven. Siden en blekkspruts arm er smal ytterst og blir bredere og bredere jo nærmere hodet den kommer, øker jeg radiusen littegrann for hver sylinder som tegnes. For å få en så glatt og jevn arm som mulig valgte jeg også å la radiusen til hver sylinder øke like mye fra ytterst til innerst som forskjellen på radiusen fra en sylinder til den neste. Lengden på hver sylinder er også avgjørende for glattheten på armens overflate. Dette har jeg etter mye prøving og feiling beregnet ved å ta 2 (avstanden i x-retningen fra starten til slutten på den første armen) og dele på antall sylindere (80) og så legge til "litt" (0.075) siden armen er bøyd, og kurven dermed er litt lengre enn avstanden i x-retningen tilsier. Siden en sylinder er hul, vil også en rekke med sylindere være hul. For å unngå at dette vises, valgte jeg å legge en liten kule ytterst i hver arm.

Etter at èn arm var laget var resten lett. Jeg lagde en metode som setter opp 8 forskjellige sett med bezierkurver avhengig av hva som er gitt som parameter (en integer mellom 0 og 7). Så lagde jeg en løkke som går fra 0 til 7 rundt while-løkken som setter opp aksene og tegner sylinderne. For hver runde i denne ytre løkken kaller jeg metoden som setter opp bezierkurven med en ny verdi, og roterer 45 grader om y-aksen i det opprinnelige koordinatsystemet.

Bildene under viser det endelige resultatet med armene først sett fra siden og så litt ovenfra. For å forenkle modelleringen lot jeg armene møtes på midten, slik at jeg slipper å bekymre meg for hvordan blekkspruten ser ut på undersiden.

For å få til en animasjon har jeg tegnet blekkspruten på en GLAnimCanvas. Denne canvasen har en innebygd "motor" som kan slås av og på, og som gjør at canvasen tegnes om igjen med eventuelle forandringer når "motoren" er igang.

Bildeserien under viser hvordan armene på blekkspruten beveger seg når den svømmer. Når armene er helt utspente, snur de og inntar de samme posisjonene i omvendt rekkefølge og danner dermed en "pumpebevegelse" i tillegg til at armene beveger seg flytter jeg hele blekkspruten oppover og bakover når armene pumper nedover (presser "vannet" unna), og litt nedover når armene pumper oppover.

Koden for å gjøre dette er ganske enkel. Jeg vedlikeholder en variabel frameCounter for å holde orden på armbevegelsene, denne økes for hver gang canvasen tegnes på nytt og slik bestemmes hvilken posisjon armene skal ha. Når armene har gått en runde (fra sammen til utspent og så sammen igjen) nullstilles frameCounter, og bevegelsen gjentas. Armenes posisjon beregnes ved at avstanden mellom kontrollpunktene når armene er helt sammen og helt utspent deles på det antallet flyttinger som skal gjøres, i dette tilfellet 5 hver vei. Dette tallet trekkes så fra eller legges til det opprinnelige kontrollpunktet når armene pumper den ene veien, og motsatt når armene pumper den andre veien. For å flytte blekkspruten vedlikeholdes to variabler, movey og movez, som brukes til å flytte i henholdsvis y- og z-retningen.

private void swim() {
  /* Svømmepunkter: (armer samlet)
  End (0, 0.5f, 0), Control2 (-0.5f, -0.25f, 0), Control1 (0, -1, 0), Start (-0.25f, -1.75f, 0).
  Flytepunkter: (armer utspent)
  End (0, 0, 0), Control2 (-1, 0.1f, 0), Control1 (-1.5f, -0.25f, 0), Start (-2, 0, 0).
  */

  // Reset frameCounter for ny svømmebevegelse
  if(frameCounter > 10) frameCounter = 1;

  // Manipulerer alle kontrollpunktene til å nærme seg utspent armposisjon
  if(frameCounter <= 5) {
    g_vEndPoint = new CVector3(0, esy -= 0.05f, 0);
    g_vControlPoint2 = new CVector3(c2sx -= 0.1f, c2sy += 0.07f, 0);
    g_vControlPoint1 = new CVector3(c1sx -= 0.3f, c1sy += 0.15f, 0);
    g_vStartPoint = new CVector3(ssx -= 0.35f, ssy += 0.35f, 0);


    incFac -= 0.0005f; // Armene er kortere i flyteposisjon, og radiusen økes mindre

    // Flytter blekkspruten litt nedover i flyteposisjonen
    movey -= 0.01f;

  // Manipulerer alle kontrollpunktene til å nærme seg samlet armposisjon
  } else {
    g_vEndPoint = new CVector3(0, esy += 0.05f, 0);
    g_vControlPoint2 = new CVector3(c2sx += 0.1f, c2sy -= 0.07f, 0);
    g_vControlPoint1 = new CVector3(c1sx += 0.3f, c1sy -= 0.15f, 0);
    g_vStartPoint = new CVector3(ssx += 0.35f, ssy -= 0.35f, 0);


    incFac += 0.0005f; // Armene er litt lengre når de er samlet, og radiusen økes mer

    // Flytter blekkspruten opp og bakover
    movey += 0.125f;
    movez -= 0.2f;
  }

  // Setter opp beziermatrisene på nytt med de nye kontrollpunktene
  makeBezier(g_vStartPoint, g_vControlPoint1, g_vControlPoint2, g_vEndPoint);
  make_d_Bezier(g_vStartPoint, g_vControlPoint1, g_vControlPoint2, g_vEndPoint);
}
    

Økningen i frameCounter og flyttingen i henhold til movey og movez skjer i display-metoden, som er der canvasen tegnes på nytt. Hvis brukeren velger å stoppe bevegelsen, resettes movey og movez, canvasens "motor" stoppes, og blekkspruten tegnes på nytt med de opprinnelige arm-kurvene. Hvis brukeren ikke stopper svømmebevegelsen, forsvinner blekkspruten etterhvert ut av skjermen.

Animasjonen i blekksprut-programmet er ikke spesielt forseggjort. Dette skyldes først og fremst at tiden ikke strakk til siden det er veldig mye stoff å sette seg inn i på relativt kort tid.

[Testprogram for frames] [Blekkspruten]

For å se hva som skjer med forskjellige figurer som tegnes langs en kurve, utviklet jeg et lite testprogram, Pearls. Dette inneholder en enkel bezierkurve, og en filmeny som lar deg velge om du vil tegne perler, bokser eller akser langs kurven, og om du vil ha aksene rotert i henhold til kurven eller ikke. Jeg har i tillegg implementert musehåndtering, slik at man kan se kurven og figurene fra alle vinkler.

Jeg har ikke beskrevet dette programmet her, bare brukt noen screenshots for å illustrere poenger i avsnittet om frames. Men metoden for å sette opp kurven og tegne figurene er den samme som for sylinderne i blekksprutprogrammet, den eneste forskjellen er kontrollpunktene til kurven og antallet figurer.

Hele dette prosjektet bærer litt preg av "geriljaprogrammering" siden den intensive formen på kurset gjorde at jeg måtte begynne å programmere uten at jeg egentlig visste hva jeg gjorde. Jeg har prøvd å rydde i det så godt det går, og delt det inn i flere klasser for å få det mer oversiktlig, men jeg ser helt klart at dette kunne vært gjort bedre hvis det hadde blitt gjort sånn helt fra begynnelsen av. på den annen side er koden rikelig kommentert og godt oppdelt, så det skulle ikke være noe problem å lese den.

Funksjonaliteten i blekksprutprogrammet er ikke overveldende, men musehåndtering er implementert slik at den kan beundres fra alle vinkler. i tillegg er det en liten meny der man kan sende blekkspruten på svømmetur og hente den tilbake til utgangsposisjonen igjen.

i tillegg til API doc'en, er koden rikelig kommentert på norsk. Det meste som har med OpenGL å gjøre er kommentert, og ikke bare de aspektene som er omtalt i denne modulen. Den "vanlige" kjente javakoden er ikke kommentert i like stor utstrekning.

Her er det helt klart rom for store utvidelser og forbedringer, ettersom tiden ble knapp og utfordringene mange...

• Lage en bedre, finere og mer dynamisk animasjon
• La blekkspruten sprute blekk, det bør de jo kunne...
• Lage en finere tekstur, det er vanskelig å få til en som får frem "dybden" i bildet
• Lage omgivelser: sjøbunn, vann, luftbobler, småfisk etc.
• Legge på skygge
• Få til mer "realistiske" ansiktstrekk, ved feks å lage hulrom til øynene