Torus

Hva

Smultringen er komplett beskrevet ved de to aktuelle radiene: en hovedradius på R og radien i selve smultringens kropp r. Vi ønsker å finne to parametre som kombinerer de to rotasjonene som er nødvendige for å identifisere et punkt entydig, en om hovedaksen og en om selve smultiringkroppens akse.

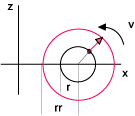
Vi lar w beskrive rotasjonen om selve smultringens hovedakse, "hullet", og lar v beskrive rotasjonen rundt selve smultringkroppen. Vi tegner smultringen i to projeksjoner:

torus

Ved å studere de to projeksjonene kan vi overbevise oss om at punktet p's koodinater er:

  z=r.sin(v)
  y=(R+r·cos(v))sin(w)
  x=(R+r·cos(v))cos(w)

Vi kan altså beskrive et vilket som helst punkt på smultringensoverflate ved de tre parametriske ligningene ovenfor. Da er vi også i stand til å avgrense flater på smultringoverflaten med nødvendig presisjon.

Flatene i smultringen kan genereres som polygoner der vi lar de to rotasjonsvinkelene gjennomløpe en full sirkel i en dobbeltløkke. Normalen i hvert punkt kan vi finne ved å tenke oss en "omhyllende" smultring. Normaler vil gå fra den indre smultringen til den ytre, med samme vinkelverdier.

public void drawTorus(float R, float r, int N, int n)
{
int maxn= 1000; // max precision
n=Math.min(n,maxn-1);
N=Math.min(N,maxn-1);
float rr=1.5f*r;
double dv=2*Math.PI/n;
double dw=2*Math.PI/N;
double v=0.0f;
double w=0.0f;
// outer loop
while(w<2*Math.PI+dw)
{
    v=0.0f;
    gl.glBegin(GL.GL_TRIANGLE_STRIP);
    // inner loop
    while(v<2*Math.PI+dv)
    {
        gl.glNormal3d(
                (R+rr*Math.cos(v))*Math.cos(w)-(R+r*Math.cos(v))*Math.cos(w),
                (R+rr*Math.cos(v))*Math.sin(w)-(R+r*Math.cos(v))*Math.sin(w),
                (rr*Math.sin(v)-r*Math.sin(v)));
        gl.glVertex3d((R+r*Math.cos(v))*Math.cos(w),
                   (R+r*Math.cos(v))*Math.sin(w),
                    r*Math.sin(v));
        gl.glNormal3d(
                (R+rr*Math.cos(v+dv))*Math.cos(w+dw)-(R+r*Math.cos(v+dv))*Math.cos(w+dw),
                (R+rr*Math.cos(v+dv))*Math.sin(w+dw)-(R+r*Math.cos(v+dv))*Math.sin(w+dw),
                rr*Math.sin(v+dv)-r*Math.sin(v+dv));
        gl.glVertex3d((R+r*Math.cos(v+dv))*Math.cos(w+dw),
                   (R+r*Math.cos(v+dv))*Math.sin(w+dw),
                    r*Math.sin(v+dv));
        v+=dv;
    } // inner loop
    gl.glEnd();
    w+=dw;
    } //outer loop
}

Tegnestrategien over kan klart effektiviseres. Ved å ta vare på verdier for "neste" runde kan vi redusere antall beregninger. Vi bør dessuten absolutt lage dislaylister.

DisplayLister

Introduksjon displaylists er gansle rett fram. Vi produserer lista når vi initialiserer:

final static int THE_TORUS=5;
...
theTorus=new oneTorus(gl);
gl.glNewList(THE_TORUS, GL.GL_COMPILE);
	theTorus.drawTorus(3.0f, 1.0f, 20, 20);
gl.glEndList();

Vi bruker listene når vi tegner:

...
stdMaterials.setMaterial(gl, stdMaterials.MAT_EMERALD, GL.GL_FRONT);
gl.glCallList (THE_TORUS);
gl.glTranslatef(4.0f,0.0f,0.0f);
gl.glRotatef(90.0f,1.0f,0.0f,0.0f);
stdMaterials.setMaterial(gl, stdMaterials.MAT_GOLD, GL.GL_FRONT);
gl.glCallList (THE_TORUS);
...

Dette programmet inneholder bådetegnemetodene og main i samme kodefil. Koden er ganske lik standard programmet som genereres av NetBeans: JOGL Application. Det som er lagt til er MouseListenerog MouseMotionListener.

package torus;
import com.sun.opengl.util.Animator;
import java.awt.Dimension;
import java.awt.Frame;
import java.awt.event.MouseEvent;
import java.awt.event.MouseListener;
import java.awt.event.MouseMotionListener;
import java.awt.event.WindowAdapter;
import java.awt.event.WindowEvent;
import javax.media.opengl.GL;
import javax.media.opengl.GLAutoDrawable;
import javax.media.opengl.GLCanvas;
import javax.media.opengl.GLEventListener;
import javax.media.opengl.glu.GLU;

/**
 * Torus.java
 */
public class Torus implements GLEventListener, 
                             MouseListener, 
                             MouseMotionListener{
    public static void main(String[] args) {
        Frame frame = new Frame("Drawing a torus");
        GLCanvas canvas = new GLCanvas();
        canvas.addGLEventListener(new Torus());
        frame.add(canvas);
        frame.setSize(640, 480);
        final Animator animator = new Animator(canvas);
        frame.addWindowListener(new WindowAdapter() {
            @Override
            public void windowClosing(WindowEvent e) {
                // Run this on another thread than the AWT event queue to
                // make sure the call to Animator.stop() completes before
                // exiting
                new Thread(new Runnable() {
                    public void run() {
                        animator.stop();
                        System.exit(0);
                    }
                }).start();
            }
        });
        // Center frame
        frame.setLocationRelativeTo(null);
        frame.setVisible(true);
        animator.start();
    }
    
    // rotating the scene
    private float view_rotx = 20.0f;
    private float view_roty = 30.0f;
    // remember last mouse position
    private int oldMouseX;
    private int oldMouseY;
    
    oneTorus theTorus;
    // naming the display list
    final static int THE_TORUS=5;
    public void init(GLAutoDrawable drawable)
    {
        GL gl = drawable.getGL();
        // Enable VSync
        gl.setSwapInterval(1);
        
        gl.glShadeModel(GL.GL_SMOOTH);
        gl.glClearColor(1.0f, 1.0f, 1.0f, 0.0f);
        // prepare ligthsource
        float ambient[] = {0.4f,0.4f,0.4f,1.0f };
        float diffuse[] = {1.0f,1.0f,1.0f,1.0f };
        float light_specular[]={1.0f,1.0f,1.0f,1.0f};
        float position[] = {40.0f,30.0f,20.0f,0.0f };
        gl.glLightfv(GL.GL_LIGHT0, GL.GL_AMBIENT,ambient,0);
        gl.glLightfv(GL.GL_LIGHT0, GL.GL_DIFFUSE, diffuse,0);
        gl.glLightfv(GL.GL_LIGHT0,GL.GL_SPECULAR,light_specular,0);
        gl.glLightfv(GL.GL_LIGHT0, GL.GL_POSITION, position,0);
        gl.glEnable(GL.GL_LIGHTING);
        gl.glEnable(GL.GL_LIGHT0);
        gl.glEnable(GL.GL_DEPTH_TEST);
        drawable.addMouseListener(this);
        drawable.addMouseMotionListener(this);
        theTorus=new oneTorus(gl);
        gl.glNewList(THE_TORUS, GL.GL_COMPILE);
            theTorus.drawTorus(3.0f, 1.0f, 30, 30);
        gl.glEndList();
    }
    public void reshape(GLAutoDrawable drawable, int x, int y, int width, int height) {
        GL gl = drawable.getGL();
        GLU glu = new GLU();
        if (height <= 0)
            height = 1;
        final float h = (float) width / (float) height;
        gl.glViewport(0, 0, width, height);
        gl.glMatrixMode(GL.GL_PROJECTION);
        gl.glLoadIdentity();
        glu.gluPerspective(45.0f, h, 1.0, 200.0);
        gl.glMatrixMode(GL.GL_MODELVIEW);
        gl.glLoadIdentity();
    }
    public void display(GLAutoDrawable drawable) {
        GL gl = drawable.getGL();
         // Clear the drawing area
        gl.glClear(GL.GL_COLOR_BUFFER_BIT | GL.GL_DEPTH_BUFFER_BIT);
        // Reset the current matrix to the "identity"
        gl.glLoadIdentity();
        gl.glTranslatef(0.0f,0.0f,-15.0f);
        gl.glRotatef(view_rotx, 1.0f, 0.0f, 0.0f);
        gl.glRotatef(view_roty, 0.0f, 1.0f, 0.0f);
        
        stdMaterials.setMaterial(gl, stdMaterials.MAT_GOLD, GL.GL_FRONT);
        gl.glCallList (THE_TORUS);
        gl.glTranslatef(4.0f,0.0f,0.0f);
        gl.glRotatef(90.0f,1.0f,0.0f,0.0f);
        stdMaterials.setMaterial(gl, stdMaterials.MAT_BRASS, GL.GL_FRONT);
        gl.glCallList (THE_TORUS);
        // Flush all drawing operations to the graphics card
        gl.glFlush();
    }
    public void displayChanged(GLAutoDrawable drawable, 
                              boolean modeChanged,
                              boolean deviceChanged) {
    }

    public void mouseClicked(MouseEvent e) {}
    public void mouseEntered(MouseEvent e) {}
    public void mouseExited(MouseEvent e) {}
    public void mouseReleased(MouseEvent e) { }
    public void mouseMoved(MouseEvent e) {}
    public void mousePressed(MouseEvent e) {
        oldMouseX = e.getX();
        oldMouseY = e.getY();
    }
    public void mouseDragged(MouseEvent e) {
        int x = e.getX();
        int y = e.getY();
        Dimension size = e.getComponent().getSize();
        float thetaY = 360.0f * ( (float)(x-oldMouseX)/(float)size.width);
        float thetaX = 360.0f * ( (float)(oldMouseY-y)/(float)size.height);
        oldMouseX = x;
        oldMouseY = y;
        view_rotx += thetaX;
        view_roty += thetaY;
    }
}

Form

Deler av hovedklassen

public class TorusAgain extends JFrame {
    // mousing around
    float oldMouseX ;
    float oldMouseY;
    float view_rotx;
    float view_roty;
    // the Renderer
    GLRenderer glr;
    /** Creates new form MainFrame */
    public TorusAgain() {
        initComponents();
        setTitle("Zoomable");
        glr=new GLRenderer();
        panel.addGLEventListener(glr);
        this.addWindowListener(new WindowAdapter() {
            @Override
            public void windowClosing(WindowEvent e) {
                System.exit(0);
            }
        });
    }
    ....
    
    private void jSliderZoomStateChanged(ChangeEvent evt) {//GEN-FIRST:event_jSliderZoomStateChanged
        glr.doIt(view_rotx, view_roty, jSliderZoom.getValue());
        panel.display();
    }//GEN-LAST:event_jSliderZoomStateChanged
    private void panelMousePressed(MouseEvent evt) {//GEN-FIRST:event_panelMousePressed
        oldMouseX = evt.getX();
        oldMouseY = evt.getY();
    }//GEN-LAST:event_panelMousePressed
    private void panelMouseDragged(MouseEvent evt) {//GEN-FIRST:event_panelMouseDragged
        int x = evt.getX();
        int y = evt.getY();
        Dimension size = evt.getComponent().getSize();
        float thetaY = 360.0f * ( (float)(x-oldMouseX)/(float)size.width);
        float thetaX = 360.0f * ( (float)(oldMouseY-y)/(float)size.height);
        oldMouseX = x;
        oldMouseY = y;
        view_rotx += thetaX;
        view_roty += thetaY;
        glr.doIt(view_rotx, view_roty,jSliderZoom.getValue());
        panel.display();
    }//GEN-LAST:event_panelMouseDragged
 ....
    
    public static void main(String args[]) {
          TorusAgain frame = new TorusAgain();
          frame.setVisible(true);
    }

The renderer:

package torus;
import javax.media.opengl.GL;
import javax.media.opengl.GLAutoDrawable;
import javax.media.opengl.GLEventListener;
import javax.media.opengl.glu.GLU;

public class GLRenderer implements GLEventListener {
    // zooming
    private float zoom_dist;
    // rotating the scene
    private float view_rotx;
    private float view_roty;
    // the torus and its displaylist name
    oneTorus theTorus;
    final static int THE_TORUS=5;
    public void init(GLAutoDrawable drawable) {
        GL gl = drawable.getGL();
        // Enable VSync
        gl.setSwapInterval(1);
        zoom_dist=20.0f;
        view_rotx = 20.0f;
        view_roty = 30.0f;
        gl.glShadeModel(GL.GL_SMOOTH);
        gl.glClearColor(1.0f, 1.0f, 1.0f, 0.0f);
        // prepare ligthsource
        float ambient[] = {0.4f,0.4f,0.4f,1.0f };
        float diffuse[] = {1.0f,1.0f,1.0f,1.0f };
        float position[] = {40.0f,30.0f,20.0f,0.0f };
        gl.glLightfv(GL.GL_LIGHT0, GL.GL_AMBIENT,ambient,0);
        gl.glLightfv(GL.GL_LIGHT0, GL.GL_DIFFUSE, diffuse,0);
        gl.glLightfv(GL.GL_LIGHT0, GL.GL_POSITION, position,0);
        gl.glEnable(GL.GL_LIGHTING);
        gl.glEnable(GL.GL_LIGHT0);
        gl.glEnable(GL.GL_DEPTH_TEST);
        theTorus=new oneTorus(gl);
        gl.glNewList(THE_TORUS, GL.GL_COMPILE_AND_EXECUTE);
        theTorus.drawTorus(3.0f, 1.0f, 20, 20);
        gl.glEndList();
    }
    public void reshape(GLAutoDrawable drawable,
                        int x, int y, int width, int height)
    {
        GL gl = drawable.getGL();
        GLU glu = new GLU();
        if (height <= 0)
            height = 1;
        final float h = (float) width / (float) height;
        gl.glViewport(0, 0, width, height);
        gl.glMatrixMode(GL.GL_PROJECTION);
        gl.glLoadIdentity();
        glu.gluPerspective(45.0f, h, 1.0, 200.0);
        gl.glMatrixMode(GL.GL_MODELVIEW);
        gl.glLoadIdentity();
    }
    public void display(GLAutoDrawable drawable)
    {
        GL gl = drawable.getGL();
         // Clear the drawing area
        gl.glClear(GL.GL_COLOR_BUFFER_BIT | GL.GL_DEPTH_BUFFER_BIT);
        // Reset the current matrix to the "identity"
        gl.glLoadIdentity();
        gl.glTranslatef(0.0f,0.0f,-zoom_dist);
        gl.glRotatef(view_rotx, 1.0f, 0.0f, 0.0f);
        gl.glRotatef(view_roty, 0.0f, 1.0f, 0.0f);
        stdMaterials.setMaterial(gl, stdMaterials.MAT_EMERALD, GL.GL_FRONT);
        gl.glCallList (THE_TORUS);
        gl.glTranslatef(4.0f,0.0f,0.0f);
        gl.glRotatef(90.0f,1.0f,0.0f,0.0f);
        stdMaterials.setMaterial(gl, stdMaterials.MAT_GOLD, GL.GL_FRONT);
        gl.glCallList (THE_TORUS);
        gl.glFlush();
    }
    public void displayChanged(GLAutoDrawable drawable, 
                                boolean modeChanged,
                                boolean deviceChanged)
    { }
    /**
     * Set the parameters we can control for the rendering
     */
    public void doIt(float x,float y,float zdist)
    {
        view_rotx=x;
        view_roty=y;
        zoom_dist=zdist;
    }
}

kode

Det animerte, musedrevne prosjektet(JOGL/Netbeans): https://svnit.hiof.no/svn/psource/JOGL/torus
prosjektet med grafikken på en form(JOGL/Netbeans): https://svnit.hiof.no/svn/psource/JOGL/torusAgain