De Casteljau
Flytt de blå kontrollpunktene og dra tallet nederst for å endre t. Den røde sirkelen viser det punktet som beregnes for en gitt t og de 4 kontrollpunktene,
P(t)=(1-t)3P0+3t(1-t)2P1+3t2(1-t)P2+t3P3
|
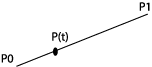
P(t)=(1-t)P0+tP1 |
|
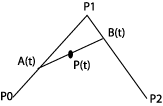
A(t)=(1-t)P0+tP1 B(t)=(1-t)P1+tP2 P(t)=(1-t)A(t)+tB(t) P(t)=(1-t)2P0+2t(1-t)P1+t2P2 |
|
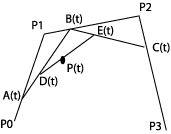
A(t)=(1-t)P0+tP1 B(t)=(1-t)P1+tP2 C(t)=(1-t)P2+tP3 D(t)=(1-t)A(t)+tB(t) E(t)=(1-t)B(t)+tC(t) P(t)=(1-t)D(t)+tE(t) P(t)=(1-t)3P0+3t(1-t)2P1+3t2(1-t)P2+t3P3 |
Javascriptet som lastes når siden er lastet og drar det hele er slik:
_test3.js
// set up a stage
var stage = new Kinetic.Stage({
// the id of the div we will host this in
container: 'test3',
width: 350,
height: 400
});
// just to hold a point
function Point(x,y){this.x=x; this.y=y;}
// controlpnts radius
var cRadius=10;
// t-value running between 0 an 1
var tValue=0.0;
//--------------------------
// make layers: background, controlpoints, curve and slider
var controlLayer = new Kinetic.Layer({x:0,y:0,width:stage.getWidth(),height:stage.getHeight()-50,opacity:0.5});
var curveLayer= new Kinetic.Layer({x:0,y:0,width:stage.getWidth(),height:stage.getHeight()-50});
var background = new Kinetic.Layer();
var sliderLayer= new Kinetic.Layer({x:0,y:stage.getHeight()-50,width:stage.getWidth(),height:50,opacity:0.5});
// draw the casteljau construction in a context, dc
function drawCasteljau(dc)
{
var A=new Point((1-tValue)*cp[0].getX()+tValue*cp[1].getX(),(1-tValue)*cp[0].getY()+tValue*cp[1].getY());
var B=new Point((1-tValue)*cp[1].getX()+tValue*cp[2].getX(),(1-tValue)*cp[1].getY()+tValue*cp[2].getY());
var C=new Point((1-tValue)*cp[2].getX()+tValue*cp[3].getX(),(1-tValue)*cp[2].getY()+tValue*cp[3].getY());
var D=new Point((1-tValue)*A.x+tValue*B.x,(1-tValue)*A.y+tValue*B.y);
var E=new Point((1-tValue)*B.x+tValue*C.x,(1-tValue)*B.y+tValue*C.y);
var P=new Point((1-tValue)*D.x+tValue*E.x,(1-tValue)*D.y+tValue*E.y);
dc.setAttr('strokeStyle','blue');
dc.setAttr('lineWidth',0.2);
dc.moveTo(cp[0].getX(),cp[0].getY());
dc.lineTo(cp[1].getX(),cp[1].getY());
dc.lineTo(cp[2].getX(),cp[2].getY());
dc.lineTo(cp[3].getX(),cp[3].getY());
dc.stroke();
dc.moveTo(A.x,A.y); dc.lineTo(B.x,B.y);dc.stroke();
dc.moveTo(B.x,B.y); dc.lineTo(C.x,C.y);dc.stroke();
dc.moveTo(D.x,D.y); dc.lineTo(E.x,E.y);dc.stroke();
dc.beginPath();
dc.arc(P.x, P.y, 7, 0, 2 * Math.PI, false);
dc.setAttr('fillStyle','red');
dc.fill();
}
// draw the bezier curve
// just pick up the context and draw as normal in a canvas
function drawCurve() {
var context = curveLayer.getContext();
context.clear();
drawCasteljau(context,tValue);
context.beginPath();
context.moveTo(cp[0].getX(), cp[0].getY());
context.bezierCurveTo(cp[1].getX(), cp[1].getY(),cp[2].getX(), cp[2].getY(),cp[3].getX(), cp[3].getY());
context.setAttr('strokeStyle','black');
context.setAttr('lineWidth',4);
context.stroke();
}
//----------------------------
// controlpoints
var cp=new Array();
cp[0]=new Kinetic.Circle({x:40,y:controlLayer.getHeight()-cRadius,radius:cRadius,
fill:'blue',stroke: 'black', strokeWidth: 1,
dragBoundFunc:function(pos){
return({x:pos.x, y:Math.min(pos.y,controlLayer.getHeight())})}
});
cp[1]=new Kinetic.Circle({x:40,y:50,radius:cRadius,
fill:'blue',stroke: 'black', strokeWidth: 1,
dragBoundFunc:function(pos){
return({x:pos.x, y:Math.min(pos.y,controlLayer.getHeight())})}
});
cp[2]=new Kinetic.Circle({x:stage.getWidth()-40,y:50,radius:cRadius,
fill:'blue',stroke: 'black', strokeWidth: 1,
dragBoundFunc:function(pos){
return({x:pos.x, y:Math.min(pos.y,controlLayer.getHeight())})}
});
cp[3]=new Kinetic.Circle({x:stage.getWidth()-40,y:controlLayer.getHeight()-cRadius,radius:cRadius,
fill:'blue',stroke: 'black', strokeWidth: 1,
dragBoundFunc:function(pos){
return({x:pos.x, y:Math.min(pos.y,controlLayer.getHeight())})}
});
// make them draggable and place them in control layer
for(var ix=0;ix < cp.length;ix++){
var theP=cp[ix];
theP.setDraggable(true);
theP.on('mouseover touchstart', function() {
//document.body.style.cursor = 'pointer';
stage.container().style.cursor= 'pointer';
});
// make on top
theP.on('mouseout', function() {
stage.container().style.cursor= 'default';
});
theP.on("dragend",function(){
drawCurve();}
);
controlLayer.add(theP);
}
//-------------------------
// set up the background
var back = new Kinetic.Rect({
x:0, y:0, width:stage.getWidth(), height:stage.getHeight(),
fill: '#ffffee', stroke: 'black', strokeWidth: 1,
});
background.add(back);
//------------------
//set up the slider
var boxT=new Kinetic.Text({
x:0, y:10, width:4*cRadius, height:40,
text:"0.0",
fontSize:20,
fill: 'blue', stroke: 'black', strokeWidth: 1,
dragBoundFunc:function(pos){
tValue=(pos.x+cRadius)/sliderLayer.getWidth();
drawCurve();
boxT.setText(tValue.toFixed(1));
return({x:Math.max(pos.x,-2*cRadius), y:sliderLayer.getY()+10})}
});
boxT.setDraggable(true);
boxT.on('mouseover touchstart', function() {
//document.body.style.cursor = 'pointer';
stage.container().style.cursor= 'pointer';
});
boxT.on('mouseout touchend', function() {
stage.container().style.cursor= 'default';
});
sliderLayer.add(boxT);
//-----------------
//update curve when draing controlpoints
controlLayer.on('beforeDraw', function() {
drawCurve();
});
//-------------------
// lets get on stage
stage.add(background);
stage.add(curveLayer);
stage.add(controlLayer);
stage.add(sliderLayer);
drawCurve();
Du kan teste og inspisere koden på en enklere webside:
test3.html
https://borres.hiof.no/wep/can/kincast/test3.html