Himmel - grunnleggende

Prinsippet bak himmelen er å tegne "sirkelbånd". Først tegnes det minste båndet (minst radius) helt på toppen av halvkulen, så tegnes sirkler med større og større radius nedover z-aksen. Radiusen økes med en konstant faktor. Mellom sirklene blir det tegnet opp triangler. Jo større avstanden mellom sirklene er på z-aksen, jo brattere vil kulen bli.

De svarte strekene er sirkler, de røde strekene er "veggene" eller trianglene som blir tegnet mellom hver sirkel.

Hver sirkel har blir tegnet med formlene:

x-verdier = cos((2*PI)*i)*radius
y-verdier = sin((2*PI)*i)*radius

Hvor "i" har verdier mellom 0 og 1 (0 er starten av sirkelen, 1 er slutten)
"radius" er selvsagt radius til sirkelen, jo høyere verdi, jo strørre sirkel.

Z-verdien som skal bestemme formen på halvkulen kan bli gitt av mange forskjellige formler. Alt etter hvor bratt eller slak kurve en vil ha. F.eks.

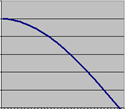
cos(PI/2*i) i - verdi mellom [0,1]. Gir en ganske slak kurve på veggen

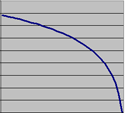
log(i) i - løper fra maxverdi til 0. Gir et en bratt kurve på veggen og slak på taket.

Jeg valgte å bruke formelen log(i), det gir muligheten til å flytte terrenget høyere opp mot taket av himmelen og dermed skjule bakgrunnen slik at man ikke ser den selv om man flytter kameraet høyt over bakken og man kan også ha kameraet høyere over bakken ut mot sidene uten at det går gjennom himmelen.

La oss se litt på koden

//Array for å holde på punktene til himmelen
float[][][] sphere = new float[37][37][3];

public void setData(float maxrad, float stride, float area, float maxheight)
{


//maxradius av ringene
float rad = ((float)maxrad*stride)/area;
//setter tmp til maxverdi (37 ringer)
float tmp = 37.0f;

for (int i = 0; i < 37; i++)
{


for (int j = 0; j < 37; j++)
{
	//x verdi
	sphere[i][j][0] =
	((float)Math.cos(2*Math.PI*((double)(j*10)/360)))
	*(float)i/37*rad;
	//y verdi
	sphere[i][j][1] =
	((float)Math.sin(2*Math.PI*((double)(j*10)/360)))
	*(float)i/37*rad;
	//Setter z verdi til log(tmp)
	sphere[i][j][2] = (float)Math.log(tmp)*maxheight;
}
//trekker fra 1 på tmp (ned til 0)
tmp--;
}

}

maxrad - største radius av sirkel (SIZE av terreng delt på 2)
stride - stride til terreng
area - jo større jo mindre himmel

Med denne koden blir antall punkter for hver sirkel 37. Hvis rendring skal optimaliseres kan en tenke seg at de øverste ringene (minste) kan ha færre punkter. Men denne koden er som tidligere nevnt kun en introduksjon til og lage himmel.

Tekstur og opptegning

Koden for å få teksturkoordinatene er den samme som blir brukt for å få teksturkoordinatene til terrenget.

public float[][][] getTextureKoord(float repeat)
{
	float[][][] text = new float[37][37][2];
	float u = 0.0f;
	float v = 0.0f;
	float hop = (1.0f/37.0f)*repeat;
	for (int i = 0; i < 37; i++)
	{

		for (int j = 0; j < 37; j++)
		{
			text[i][j][0] = u;
			text[i][j][1] = v;

			u += hop;
		}
		v += hop;
		u = 0.0f;

	}
	return text;
}

Forskjellen er at hop = 1.0f/(antall punkter pr.sirkel) og ikke 1.0f/(terreng SIZE). Repeat er antall ganger en vil at teksturen skal gjentas på overflaten.

Opptegning og pålegging av tekstur er lik kode som ved opptegning av terreng.

public void drawSky()
{
	gl.glEnable(GL_TEXTURE_2D);
	//Legg på tekstur
	gl.glBindTexture(GL_TEXTURE_2D, skytext);
	gl.glTexEnvi(GL_TEXTURE_ENV,GL_TEXTURE_ENV_MODE,GL_DECAL);
	for (int x = 0; x < 36; x++)
	{
		gl.glBegin(GL_TRIANGLE_STRIP);
		for (int y = 0; y < 37; y++)
		{
			//Tekstur koordinater
			gl.glTexCoord2f(textureSky[x][y][0],
			textureSky[x][y][1]);
			//Vertexpoint
			gl.glVertex3f(sphere[x][y][0],
			sphere[x][y][1], sphere[x][y][2]);
			//Tekstur koordinater
			gl.glTexCoord2f(textureSky[x+1][y][0],
			textureSky[x+1][y][1]);
			//Vertexpoint
			gl.glVertex3f(sphere[x+1][y][0],
			sphere[x+1][y][1], sphere[x+1][y][2]);

		}
		gl.glEnd();
	}
}

Sphere.java