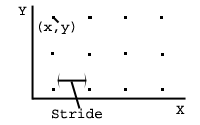
Høydekart

Alle (x,y) koordinatene ligger jevnt fordelt utover i planet med like store mellomrom (stride). Til hver (x,y) koordinat hører det til en Z-verdi i rommet, og det er denne Z-verdien som blir manipulert for å skape et 3-dimensjonalt terreng. Dette kan gjøres på mange forskjellige måter, men det skal jeg ikke gå inn på i denne delen av modulen. Ved å la (x, y) verdiene ligge jevnt fordelt på denne måten trenger vi ikke lenger bry oss om x og y verdiene, kun de tilhørende z-verdiene.

Kode for å sette opp koordinater til et høydekart:

/*
Grunnlegende oppbygning av et høydekart
*/

public class HeightField
{
   private int SIZE;    //bredde i av området(kvadratisk)

   //Array som innholder innformasjon
   //om punkter i x, y og z retning
   private float[][][] flate = new float[SIZE][SIZE][3];




   //Konstruktør for å initaliere klassen
   public HeightField(int Size, float stride)
   {
      SIZE = Size;
      setData(stride);
   }

   //Metode for å sette opp en SIZEx * SIZEy flate
   //stride er mellomrom mellom punkter
   private void setData(float stride)
   {
      float x = 0.0f;
      float y = 0.0f;

      //Alle x-koordinater
      for (int breddeX = 0; breddeX < SIZE-1; breddeX++)
      {
         //Alle y-koordinater for en x-verdi
         for (int breddeY = 0; breddeY < SIZE-1; breddeY++)
         {
            //Setter y verdi
            flate[breddeX][breddeY][0] = y;
            //Setter x verdi
            flate[breddeX][breddeY][1] = x;
            //Setter z verdi (høyde) til 0,
            //legger ikke inn høyder enda
            flate[breddeX][breddeY][2] = 0.0f;

            y += stride;
         }
         y = 0.0f;
         x += stride;
      }
   }


}

SIZE størrelsen flaten skal ha, det tilsvarer antall punkter i x og y retningen. Ved kun og sette SIZE å si at den skal bestemme både x og y blir området kvadratisk. Det er mulig å utvide programmet til å ha forskjellige verdier og gjøre området rektangulært, men det kan føre til andre problemer som med teksturer o.l. så det letteste er å holde seg til kvadratiske områder. Den faktiske bredden og høyden til flaten blir ((SIZE-1) * stride) og ((SIZE-1) * stride) siden "stride" definerer avstanden mellom punktene.
Arealet til flaten blir dermed (((SIZE-1)*stride) * ((SIZE-1)*stride)).
Hvis flaten er bygd opp av triangler blir antall triangler (SIZE-1 * SIZE-1 * 2). Hvis flaten er bygd opp av kvadrater blir antall kvadrater (SIZE-1 * SIZE-1). ("Triangler eller kvadrater" tas opp i en separat modul).

Arrayen flate[][][] innholder alle x, y og z verdier for hele flaten. Jeg har valgt og behandle dataen i en egen klasse, dette er kun oppsett og lagring av x, y og z verdier, ingen tegning på skjerm. Derfor trengs det noen metoder for å få tilgang på dataen til den delen av programmet som har ansvaret for opptegning og manipulering av z-verdier.

//Metode for å få tak i høydekart koordinater
   public float[][][] getData()
   {
      return flate;
   }

   //Metode for å få høyden i punktet (x,y)
   public float getHeight(int x, int y)
   {
      return flate[x][y][2];
   }

   //Metode for å sette høyden i punktet (x,y)
   public void setHeight(int x, int y, float verdi)
   {
      flate[x][y][2] = verdi;
   }

Her er det metodene getHeight() og setHeight() som blir de som det skal jobbes med for å skape høydeforskjellene i terrenget.

Gråskalabilder

En enkel og grei måte å lage naturtro landskap på er å bruke gråskala bilder til å manipulere Z-verdiene (høydeverdiene) til et høydekart. Ved å lese fargeverdiene til bildet i et gitt koordinat og overføre denne verdien til z-verdien i tilsvarende koordinat på høydekartet oppnår man dette resultat.

Fargen svart kan angi den laveste verdien (høyden) z kan få og helt hvitt kan angi den høyeste verdien. Eller omvendt helt etter hva en programmerer.

Gråtonene mellom helt svart og helt hvitt vil da gi lave topper og bakker. Det kan lønne seg å få ut fargeverdiene fra kartet med 0 som minste verdi og 1 som største verdi. Og heller gange med en gitt faktor for å få større høydeforskjeller.

Det man trenger er 1 stk pent gråskalabilde. Det kan man få med f.eks. og bruke programmet Terragen til å generere det for deg, eller lage det selv i f.eks Adobe Photoshop, men da er det ikke alltid like lett å få det resultatet en ønsker. Man trenger også 1 stk. høydekart, det får man ved å følge oppskriften ovenfor. Bildet er nødt til å ha likt eller flere antall piksler en antall punkter i høydekartet. Det fordi et punkt i kartet tilsvarer en høyde i høydekartet.

For å få ut pikselverdier til et bilde i java er en nødt til å laste bildet inn i et BufferedImage object. Det er fort gjort med få linjer kode

HeightField hf;
BufferedImage bi;


//Konstruktør til klassen
public HeightImageLoader(HeightField h)
{
	hf = h;
	//Setter størelsen på BufferedImage
	//til størrelsen av høydekartet
	bi = new BufferedImage(hf.getSize(),
	hf.getSize(), BufferedImage.TYPE_INT_ARGB);
}




public void loadImage(Image img)
{
	//Laster bildet inn i BufferedImage
	bi.getGraphics().drawImage (img, 0, 0, null);
}

Etter at bildet er lastet over i BufferedImage objektet er det bare å gå i gang med manipulasjonen av z-verdier i høydekartet. Pikselverdiene til bildet i punktet (x,y) hentes ut fra BufferedImage ved bruk av metoden:

int getRGB(int x, int y)

Denne metoden returnere piksel verdiene i 24-bit fargekode og derfor må vi dele på 2^24 for å få verdier mellom 0 og 1. Koden for å sette z-verdiene til høydekartet er også ganske grei.

public void setData(float diff, float level)
{
   for (int x = 0; x < hf.getSize()-1; x++)
   {
      for (int y = 0; y < hf.getSize()-1; y++)
      {
         //Får ut fargeverdi til bilde
         float height = (((float)bi.getRGB(x,y)/
         (float)Math.pow(2,24))*diff) +
         (diff+1.0f) + level;
         //Setter høydeverdi til x,y
         //punkt i høydekartet
         hf.setHeight(x, y, height);
      }
   }
}

diff - høydeforskjellen mellom laveste og høyeste punkt i høydekartet. Jo høyere verdi jo større høydeforskjeller.

level - flytter minste verdi til høydekartet oppover på z-aksen. Jo høyere verdi jo høyere opp flyttes terrenget.

Glatting av terreng

Noen ganger ser ikke terrenget så veldig pent ut bare ved å laste inn gråskalabilder for å lage fjell og daler. Det kan være skarpe kanter og for bratte stup. Da kan vi trenge og glatte fjellene for å gi terrenget et bedre utseende. Til det trenger vi en algoritme som kjører gjennom hele høydekartet og justerer høydeverdiene slik at terrenget blir glattere. En slik algoritme fant jeg på Lighthouse3d.com sine terreng tutorial sider. Men litt tilpassning til høydekartet jeg har lagd fikk jeg en enkel og bra glattingsalgoritme. Algoirtmen går igjennom alle radene først fra venstre mot høyre, så fra høyre mot venstre og justerer alle høydeverdiene i forhold til nabohøydeverdien. Deretter går den gjennom alle kolonnene, venstre mot høyre og høyre mot venstre og gjør det samme. Den viktige variabelen i denne algoritmen er k. Hvis k = 0 vil den respektive høyden bli satt til naboens høyde. Hvis k = 1 vil den respektive høyden bli det samme og terrenget ikke bli glattet. Men alle verdier mellom 0 og 1 vil terrenget bli glattet, men jo lavere verdi jo glattere og lavere vil høydene bli. Det går også an og kjøre glattingsalgoritmen flere ganger på høydekartet med en relativ høy verdi og få en bedre effekt en å kjøre den 1 gang med lav verdi. Jeg valgte k = 0.75 og kjørte algoritmen 2 ganger.

public void smooth(float k)
{
	/* Rows, left to right */
	for(int y = 0;y < hf.getSize()-1; y++)
	    for (int x = 1;x < hf.getSize()-1; x++)
		hf.setHeight(x,y,(hf.getHeight(x-1,y) * (1-k) +
			      hf.getHeight(x,y) * k));

	/* Rows, right to left*/
		for(int y = hf.getSize()-2;y < -1 ; y--)
	    for (int x = 0;x < hf.getSize()-1; x++)
		hf.setHeight(x,y,(hf.getHeight(x+1,y) * (1-k) +
			      hf.getHeight(x,y) * k));

	/* Columns, bottom to top */
	for(int x = 1;x < hf.getSize()-1; x++)
	    for (int y = 0;y < hf.getSize()-1; y++)
		hf.setHeight(x,y,(hf.getHeight(x-1,y) * (1-k) +
			      hf.getHeight(x,y) * k));

	/* Columns, top to bottom */
	for(int x = hf.getSize()-2;x < -1 ; x--)
	    for (int y = 0;y < hf.getSize()-1; y++)
		hf.setHeight(x,y,(hf.getHeight(x+1,y) * (1-k) +
			      hf.getHeight(x,y) * k));

}

Detter er samme terrenget glattet med k = 0.75, men algoritmen er kjørt forskjellig antall ganger:

Glattet 0 ganger

Glattet 5 ganger

Glattet 45 ganger

Glattinga gjøres såklart bare en gang i init() metoden, og ikke hver gang terrenget skal tegnes opp i display() metoden.

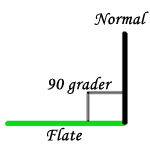
Normaler på flater

For at openGL skal kunne gjøre lysberegning på flater er vi nødt til å beregne en normal på en flate. Vanligvis gjøres dette kun ved å beregne en 90 graders normal på en rett flate.

Når vi da kobler flere flater sammen må normalene på alle flatene beregnes.

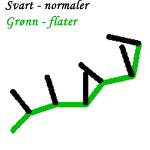
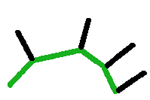
Når lysberegningene gjøres på flatene nå blir kantene mellom skjøtingene av flatene veldig tydelig. Et triks for å få skjøtene til å se (ikke faktisk bli, optisk bedrag) rundere ut er bruk av interpolering. Da blir normalene til hver flate beregnet ut i fra flaten som er skjøtet på den respektive flaten. Dette kalles interpolering og gjøres ved å beregne kryssproduktet mellom to vektorer. For mer om dette se modulen Skygge og glatting.

Her er to metoder. Den første beregner normal vanlig 90 grader på flatene, og den andre tar hensyn til de skjøtete flatene og beregner normalene interpolert. Den siste er den jeg bruker for å modellere terrenget mitt fordi den gir penest resultat.

public class Normals
{
   HeightField hf;
   float[][][] flate;
   float[][][] normaler;
   public Normals(HeightField h)
   {
      hf = h;
      flate = h.getData();
      normaler = new float[h.getSize()][h.getSize()][3];
   }

   public void calcNormals()
   {
      float a[] = new float[3];
      float b[] = new float[3];

      for (int x = 1; x < hf.getSize()-2; x++)
      {
         for (int y = 1; y < hf.getSize()-2; y++)
         {
         // make one normal for each strip
               a[0]=flate[x][y+1][0]-flate[x][y][0];
               b[0]=flate[x+1][y+1][0]-flate[x][y][0];
               a[1]=flate[x][y+1][1]-flate[x][y][1];
               b[1]=flate[x+1][y+1][1]-flate[x][y][1];
               a[2]=flate[x][y+1][2]-flate[x][y][2];
               b[2]=flate[x+1][y+1][2]-flate[x][y][2];

         normaler[x][y][0] = a[1]*b[2]-a[2]*b[1];
         normaler[x][y][1] = a[2]*b[0]-a[0]*b[2];
         normaler[x][y][2] = a[0]*b[1]-a[1]*b[0];
         }
      }
   }

   public void calcInterNormals()
   {
      float a[] = new float[3];
      float b[] = new float[3];

      for (int x = 1; x < hf.getSize()-2; x++)
      {
         for (int y = 1; y < hf.getSize()-2; y++)
         {
         // make one normal for each strip
               a[0]=flate[x][y+1][0]-flate[x][y][0];
               b[0]=flate[x+1][y+1][0]-flate[x][y][0];
               a[1]=flate[x][y+1][1]-flate[x][y][1];
               b[1]=flate[x+1][y+1][1]-flate[x][y][1];
               a[2]=flate[x][y+1][2]-flate[x][y][2];
               b[2]=flate[x+1][y+1][2]-flate[x][y][2];

            float n1[] = new float[3];
            n1[0] = a[1]*b[2]-a[2]*b[1];
            n1[1] = a[2]*b[0]-a[0]*b[2];
            n1[2] = a[0]*b[1]-a[1]*b[0];

         a[0]=flate[x+1][y-1][0]-flate[x][y][0];
         b[0]=flate[x][y-1][0]-flate[x][y][0];
               a[1]=flate[x+1][y-1][1]-flate[x][y][1];
               b[1]=flate[x][y-1][1]-flate[x][y][1];
               a[2]=flate[x+1][y-1][2]-flate[x][y][2];
               b[2]=flate[x][y-1][2]-flate[x][y][2];

            float n2[] = new float[3];
            n2[0] = a[1]*b[2]-a[2]*b[1];
            n2[1] = a[2]*b[0]-a[0]*b[2];
            n2[2] = a[0]*b[1]-a[1]*b[0];

         normaler[x][y][0] = (n1[0]*n2[0])/2.0f;
         normaler[x][y][1] = (n1[1]*n2[1])/2.0f;
         normaler[x][y][2] = (n1[2]*n2[2])/2.0f;
         }
      }
   }

   public float[][][] getNormals()
   {
      return normaler;
   }

}

Den siste metoden er nødvendig for å få normalene som er blitt beregnet tilbake til der flatene skal tegnes.

Kode

• HeightField.java
• HeightImageLoader.java
• Normals.java