Bezierkurven

Hva

Vi skal se på Bezier-kurven. Dette er en måte å tegne glatte kurveformer. Det er denne du finner i mange tegneprogrammer på datamaskinen. Formen er oppkalt etter en fransk bilingeniør, sikkert i forbindelse med design av karosseri.

Begreper som du finner i dokumentasjonen til Processing Reference

bezier(), bezierPoint()
PVector

PVector har i og for seg ikke noe med kurven å gjøre. Jeg har bare brukt denne for å lagre punkverdier, og forenkle handteringen av museposisjoner.

Relevante Skisser

bezier/bezierEnkel, bezier/bezierPerler, bezier/bezierAnimasjon

Enkel kurve

Det Processing tilbyr oss er en kurve som er bestemt av 4 styrepunkter. Kurven starter i det første sstyrepunktet og ender i det fjerde. De to andre påvirker kurven(drar i den) med en styrke som avhenger av hvor på kurven vi er. Vi kan matematisk sett lage bezierkurver med mange styrepunkter, men det vanlige når vi skal lage lengere kurver (med flere buktninger) er å skjøte enkle 4-punktskurver der det siste kontrollpunktet i den ene kurvedelen er det første i den neste. Skisssen ser slik ut, og vi kan trekke i de 4 punktene og se hvordan kurven endrer seg:

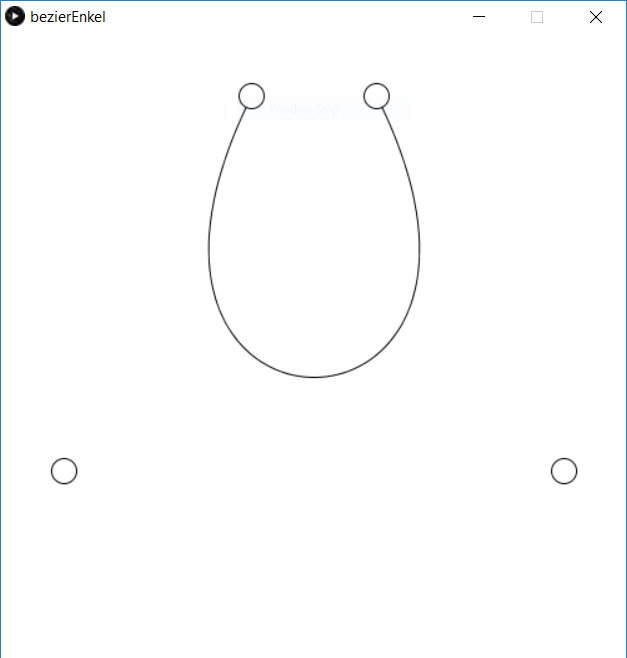
Skissen:

/**
* Tegn en enkel bezier-kurve
* kontrolpunktene kan flyttes
*/
// kontrollpunktene
PVector[] Pt;
// noen som flyttes ?
boolean[] dragged;
void setup(){
  size(500,500);
  Pt=new PVector[4]; 
  Pt[0]=new PVector(width/2 -50,50);
  Pt[1]=new PVector(50,350);
  Pt[2]=new PVector(450,350);
  Pt[3]=new PVector(width/2 +50,50);
  // er ey punkt i bevegelse
  dragged=new boolean[4];
  for(int ix=0;ix< dragged.length;ix++)
    dragged[ix]=false;
}
void draw(){
  // flytt evt et punkt til museposisjon
  for(int ix=0;ix < dragged.length;ix++)
    if(dragged[ix]){
      Pt[ix].x=mouseX;
      Pt[ix].y=mouseY;
    }
  
  background(255);
  //kurven
  noFill();
  bezier(Pt[0].x,Pt[0].y,
         Pt[1].x,Pt[1].y,
         Pt[2].x,Pt[2].y,
         Pt[3].x,Pt[3].y);
  //kontrollpunktene
  fill(255);
  ellipse(Pt[0].x,Pt[0].y,20,20);
  ellipse(Pt[1].x,Pt[1].y,20,20);
  ellipse(Pt[2].x,Pt[2].y,20,20);
  ellipse(Pt[3].x,Pt[3].y,20,20);
}
void mousePressed(){
  for(int ix=0; ix < Pt.length; ix++){
    if((mouseX > Pt[ix].x-30) && (mouseX < Pt[ix].x+30) 
     &&(mouseY > Pt[ix].y-30) && (mouseY < Pt[ix].y+30)){
       dragged[ix]=true;
       return;
     }
  }
}
void mouseReleased(){
  // få dem inn i skissen hvis vi har slept dem utenfor
  // og slutt å dra
  for(int ix=0;ix < Pt.length;ix++){
    Pt[ix].x=max(10,min(Pt[ix].x,width-10));
    Pt[ix].y=max(10,min(Pt[ix].y,height-10));
    dragged[ix]=false;
  }
}

Posisjoner på kurven

Vi vil betrakte kurven som et perlekjede og plassere noen "perler" lang kurven. For å få til dette må vi kunne finne ut hvor kurven går, i detalj. Logikken bak dette er at når Processing tegner kurven så regnes enkeltpunkter ut basert på påvirkningen fra de 4 styrepunktene. Bezier-kurven er det som kalles en parametrisk kurve og vi kan vandre langs kurven med å la en patameter endre seg i små steg fra 0 til 1. Funksjonen bezierPoint() lar oss bestemme et slikt beregningspunkt. Parameterne er de fire styrepunktene og en verdi mellom 0 og 1. Hvis den siste parameteren er 0 havner vi i det første styrepunktet, og når den er 1 havner vi i det siste. Alle verdier mellom 0 og 1 plasserer oss et sted lang skurve. Når vi regner ut et slikt punkt for hver "perle" vi vil plassere kan det bli seende slik ut:

Skissen:

/**
* Tegn en enkel bezier-kurve
* med kuler, som et perlekjede
* kontrollpunktene kan flyttes
*/
// kontrollpunktene
PVector[] Pt;
boolean[] dragged;
// perlene
float radius;
void setup(){
  size(500,500);
  radius=20;
  Pt=new PVector[4]; 
  Pt[0]=new PVector(width/2 -50,50);
  Pt[1]=new PVector(50,350);
  Pt[2]=new PVector(450,350);
  Pt[3]=new PVector(width/2 +50,50);
  dragged=new boolean[4];
  for(int ix=0;ix< dragged.length;ix++)
    dragged[ix]=false;
}
void draw(){
  for(int ix=0;ix < dragged.length;ix++)
    if(dragged[ix]){
      Pt[ix].x=mouseX;
      Pt[ix].y=mouseY;
    }
  
  background(255);
  // kurven
  noFill();
  bezier(Pt[0].x,Pt[0].y,
         Pt[1].x,Pt[1].y,
         Pt[2].x,Pt[2].y,
         Pt[3].x,Pt[3].y);
   
  // 20 perler
  // stegvis med  t
  int steg = 20;
  for (int i = 0; i <= steg; i++) {
    float t = i / float(steg);
    float x = bezierPoint(Pt[0].x, Pt[1].x, Pt[2].x, Pt[3].x, t);
    float y = bezierPoint(Pt[0].y, Pt[1].y, Pt[2].y, Pt[3].y, t);
    // perlen
    fill(255,255,0);
    ellipse(x, y, radius, radius);
  }
   
  // kontrollpunktene
  fill(255);
  ellipse(Pt[0].x,Pt[0].y,20,20);
  ellipse(Pt[1].x,Pt[1].y,20,20);
  ellipse(Pt[2].x,Pt[2].y,20,20);
  ellipse(Pt[3].x,Pt[3].y,20,20);
}
void mousePressed(){
  for(int ix=0; ix < Pt.length; ix++){
    if((mouseX > Pt[ix].x-30) && (mouseX < Pt[ix].x+30) 
     &&(mouseY > Pt[ix].y-30) && (mouseY < Pt[ix].y+30)){
       dragged[ix]=true;
       return;
    }
  }
}
void mouseReleased(){
  // få dem inn i skissen hvis vi har slept dem utenfor
  for(int ix=0;ix < Pt.length;ix++){
    Pt[ix].x=max(10,min(Pt[ix].x,width-10));
    Pt[ix].y=max(10,min(Pt[ix].y,height-10));
    dragged[ix]=false;
  }
}

Animasjon

Ved å endre uttegningen, draw, kan vi lage en animasjon av en kule som løper fram og tilbake langs bezier-kurven.

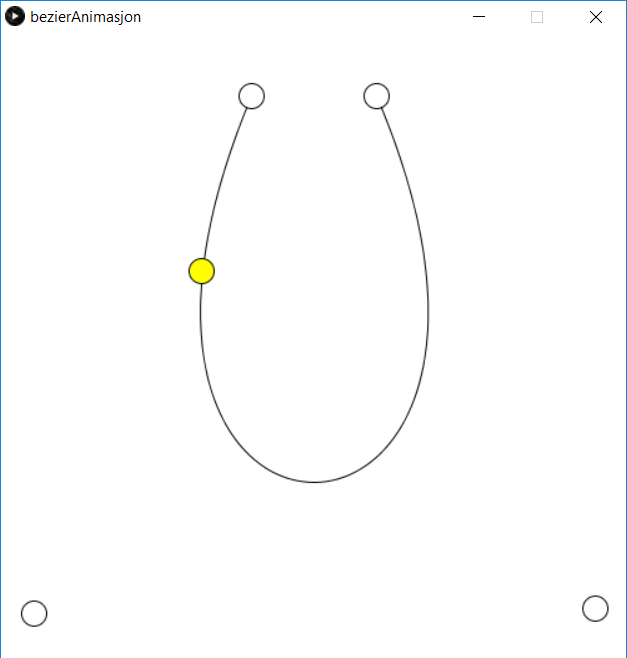
Skissen:

/**
 Tegn en enkel bezier-kurve
 Kontrollpunktene kan flyttes
 En kule vandrer langs kurven
*/
// kontrollpunktene
PVector[] Pt;
boolean[] dragged;
// flyttingen
float t,tSteg;
// perlene
float radius;
void setup(){
  size(500,500);
  radius=20;
  Pt=new PVector[4]; 
  Pt[0]=new PVector(width/2 -50,50);
  Pt[1]=new PVector(50,350);
  Pt[2]=new PVector(450,350);
  Pt[3]=new PVector(width/2 +50,50);
  dragged=new boolean[4];
  for(int ix=0;ix< dragged.length;ix++)
    dragged[ix]=false;
  t=0.0;
  tSteg=0.01;
  // du kan endre hastigheten 
  // med å sette framerate
  //frameRate(20);
}
void draw(){
  for(int ix=0;ix < dragged.length;ix++)
    if(dragged[ix]){
      Pt[ix].x=mouseX;
      Pt[ix].y=mouseY;
    }
  
  background(255);
  // kurven
  noFill();
  bezier(Pt[0].x,Pt[0].y,
         Pt[1].x,Pt[1].y,
         Pt[2].x,Pt[2].y,
         Pt[3].x,Pt[3].y);
  
  // 1 kule som vandrer langs kurven
  // stegvis langs   t
  float x = bezierPoint(Pt[0].x, Pt[1].x, Pt[2].x, Pt[3].x, t);
  float y = bezierPoint(Pt[0].y, Pt[1].y, Pt[2].y, Pt[3].y, t);
  t=t+tSteg;
  // må vi snu før neste frame?
  if(t > 1.0){
      t=1.0;
      tSteg=-tSteg;
  }
  else if(t < 0.0){
     t=0.0;
     tSteg=-tSteg;
   }
    fill(255,255,0);
    ellipse(x, y, radius, radius);
  
  // kontrollpunktene
  fill(255);
  ellipse(Pt[0].x,Pt[0].y,20,20);
  ellipse(Pt[1].x,Pt[1].y,20,20);
  ellipse(Pt[2].x,Pt[2].y,20,20);
  ellipse(Pt[3].x,Pt[3].y,20,20);
}
void mousePressed(){
  for(int ix=0; ix < Pt.length; ix++){
    if((mouseX > Pt[ix].x-30) && (mouseX < Pt[ix].x+30) 
     &&(mouseY > Pt[ix].y-30) && (mouseY < Pt[ix].y+30)){
       dragged[ix]=true;
       return;
    }
  }
}
void mouseReleased(){
  // få dem inn i skissen hvis vi har slept dem utenfor
  for(int ix=0;ix < Pt.length;ix++){
    Pt[ix].x=max(10,min(Pt[ix].x,width-10));
    Pt[ix].y=max(10,min(Pt[ix].y,height-10));
    dragged[ix]=false;
  }
}

Lengere kurve

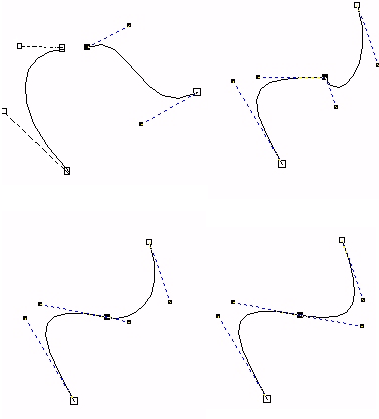
Matematisk kan vi lage formler for å tegne bezierkurver med flere styrepinkter enn fire, og derved få til flere "buktinger". Processing tilbyr oss bare denne 4-punktsløsninen. Vi kan imidlertid skøte kurver ved å la det siste styrepunktet i den enekurven falle sammen med detførste i den neste kurven. Posisjonen til de to nabokurvene bestemmer hvor glatt overgangen fra en kurve til den neste blir.

3D

Tredimensjonal tegning er ikke tema i på denne siden, men det går fint an å lage skisser av denne typen i 3 dimensjoner: